Tìm x :(x+6) chia hết cho (x-1)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
22 tháng 4 2018
a) (x + 6) - x chia hết cho x => 6 chia hết cho x hay xÎƯ(6) = {-6; -3; -2; -l; l; 2; 3; 6}.
b) ( x +9) - (x + l) chia hết cho (x + l) =>8 chia hết cho (x + l)
=> x + 1 ÎƯ (8) = { - 8; -4; -2; -1; 1; 2; 4; 8}.
Từ đó tìm được x Î {- 9; - 5; - 3; - 2; 0; 1; 3; 7}.
c) (2 + l) -2 (x - l) chia hết cho (x - l) => 3 chia hết cho (x - l)
=> x - 1Î Ư (3) = {- 3; -1; 1; 3}. Từ đó tìm được x Î{ - 2; 0; 2; 4}.
KD
7A. Tìm x ∈ Z sao cho:
a) x + 6 chia hết cho x
b) x + 9 chia hết cho x + 1
c) 2x + 1 chia hết cho x - 1
0
2 tháng 11 2016
a) 4 chia hết cho x
=> x \(\in\) Ư(4) = {1;-1;2;-2;4;-4}
Vậy x \(\in\) {1;-1;2;-2;4;-4}
b) 6 chia hết x+1
=> x+1 \(\in\) Ư(6) = {-1;1;2;-2;3;-3;6;-6}
Vậy x \(\in\) {-2;0;1;-3;2;-4;5;-7}
c) 12 chia hết cho x và 16 chia hết cho x
=> x \(\in\) ƯC(12;16) = {1;2;4}
Vậy x \(\in\) {1;2;4}
d) x chia hết cho 6 và x chia hết cho 4
=> x \(\in\) BC(6;4) = {0;12;24;48;...}
Mà 12<x<40 => x = 24
e) x+5 chia hết cho x+1
=> x+1+4 chia hết cho x+1
=> 4 chia hết cho x+1
=> x+1 \(\in\) Ư(4) = {1;-1;2;-2;4;-4}
Vậy x \(\in\) {0;-2;1;-3;3;-5}
LY
2 tháng 11 2016
b) \(6⋮x+1\)
\(\Rightarrow x+1\inƯ\left(6\right)\)
hay \(x+1\in\left\{1,2,3,6\right\}\)
Vậy \(x\in\left\{0,1,2,5\right\}\)
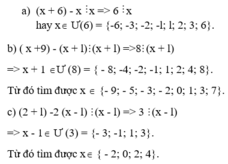
\(x+6⋮x-1\)
Ta có: \(x-1+7\)
Mà: \(x-1⋮x-1\)
=> \(7⋮x-1\)
\(\Rightarrow x-1\inƯ\left(7\right)\)
\(Ư\left(7\right)=\left\{1;-1;7;-7\right\}\)
Th1: \(x-1=1\Rightarrow x=2\)
Th2: \(x-1=-1\Rightarrow x=0\)
Th3: \(x-1=7\Rightarrow x=8\)
Th4: \(x-1=-7\Rightarrow x=-6\)
Vậy: \(x\in\left\{2;0;8;6\right\}\) thì \(x+6⋮x-1\)
\(x+6\)⋮\(x-1\)
\(x-1+7\) ⋮ \(x-1\)
7⋮ \(x-1\)
Ư(7) = {-7; -1; 1; 7}
Lập bảng ta có:
Theo bảng trên ta có:
Các giá trị của \(x\) thỏa mãn đề bài lần lượt là: -6; 0; 2; 8
Vậy \(x\) \(\in\) {-6; 0; 2; 8}