Trong đề thi THPTQG 2023 môn Toán có 50 câu trắc nghiệm, mỗi câu được 0,2 điểm. Mỗi câu hỏi có 4 đáp án trắc nghiệm A,B,C,D và chỉ có 1 đáp án đúng. Điểm bé hơn hoặc bằng 1 được coi là điểm liệt. Bạn An chọn ngẫu nhiên 4 đáp án với cả 50 câu hỏi. Tính xác suất để bạn An không bị điểm liệt.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D
Số phần tử không gian mẫu: ![]()
Gọi A là biến cố học sinh chỉ chọn đúng đáp án của 25 câu hỏi
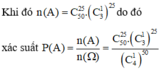

Gọi x là số câu trả lời đúng \(\Rightarrow50-x\) câu trả lời sai
Số điểm đạt được:
\(0,2.x-0,05\left(50-x\right)=4,5\)
\(\Rightarrow x=28\)
Vậy học sinh đó trả lời đúng 28 câu và trả lời sai 22 câu
Có \(C_{50}^{28}\) cách chọn 28 câu từ 50 câu
Ở mỗi câu, học sinh có \(\dfrac{1}{4}\) xác suất trả lời đúng và \(\dfrac{3}{4}\) xác suất trả lời sai
Do đó, xác suất học sinh đó được 4,5 điểm là:
\(C_{50}^{28}.\left(\dfrac{1}{4}\right)^{28}.\left(\dfrac{3}{4}\right)^{22}=...\)

Đáp án D
Học sinh đó làm đúng được 5 điểm khi làm được đúng 25 câu bất kỳ trong số 50 câu, 25 câu còn lại làm sai.
Xác suất để học sinh là đúng một câu bất kỳ là 1 4 , làm sai một câu là 3 4 . Do đó xác suất để học sinh đó làm đúng 25 câu bất kỳ trong số 50 câu là C 50 25 . 1 4 25 .
Xác suất để hoạc sinh đó làm sai 25 câu còn lại là 3 4 25 .
Vậy xác suất để học sinh đó làm được đúng 5 điểm là: C 50 25 1 4 25 . 3 4 25

Đáp án B
Học sinh đó làm đúng được 5 điểm khi làm được đúng 25 câu bất kỳ trong số 50 câu, 25 câu còn lại làm sai.
Xác suất để học sinh là đúng một câu bất kỳ là 1 4 , làm sai một câu là . Do đó xác suất để học sinh đó làm đúng 25 câu bất kỳ trong số 50 câu là C 50 25 . 1 4 25 .
Xác suất để hoạc sinh đó làm sai 25 câu còn lại là 3 4 25 .
Vậy xác suất để học sinh đó làm được đúng 5 điểm là: C 50 25 . 1 4 25 . 3 4 25

Đáp án D
Học sinh đó làm đúng được 5 điểm khi làm được đúng 25 câu bất kỳ trong số 50 câu, 25 câu còn lại làm sai.
Xác suất để học sinh là đúng một câu bất kỳ là 1 4 , làm sai một câu là 3 4 . Do đó xác suất để học sinh đó làm đúng 25 câu bất kỳ trong số 50 câu là C 50 25 . 1 4 25 .
Xác suất để hoạc sinh đó làm sai 25 câu còn lại là 3 4 25 .
Vậy xác suất để học sinh đó làm được đúng 5 điểm là: C 50 25 . 1 4 25 . 3 4 25

Chọn D.
Cách 1: Tự luận từ đầu
Để học sinh được đúng 6 điểm tức là trả lời đúng được tất cả 30 câu và trả lời sai 20 câu.
Gọi A là biến cố mà học sinh trả lời đúng được 30 câu. Trước hết ta phải chọn ra 30 câu từ 50 câu để trả lời đúng (mỗi câu đúng chỉ có 1 cách chọn) , còn lại 20 câu trả lời sai (mỗi câu sai có 3 cách chọn)


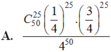
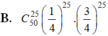
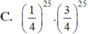
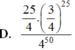

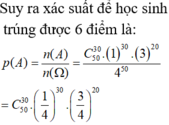
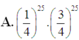
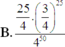

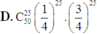
Đường link tham khảo: Có nên "khoanh lụi" thi THPTQG hay không?
https://www.youtube.com/watch?v=gETeWVaK-E8
\(n\left(\Omega\right)=4^{50}\)
Nếu bạn An bị điểm liệt thì số câu đúng mà bạn chọn được bé hơn hoặc bằng 5, hay số câu sai lớn hơn hoặc bằng 45.
Gọi biến cố A: "bạn An không bị điểm liệt"
\(n\left(\overline{A}\right)=C_{50}^{45}.3^{45}+C_{50}^{46}.3^{46}+C_{50}^{47}.3^{47}+C_{50}^{48}.3^{48}+C_{50}^{49}.3^{49}+C_{50}^{50}.3^{50}\)
Xác suất để bạn An không bị điểm liệt
\(P\left(A\right)=1-\dfrac{n\left(\overline{A}\right)}{n\left(\Omega\right)}\)
\(=1-\dfrac{C_{50}^{45}.3^{45}+C_{50}^{46}.3^{46}+C_{50}^{47}.3^{47}+C_{50}^{48}.3^{48}+C_{50}^{49}.3^{49}+C_{50}^{50}.3^{50}}{4^{50}}\)
\(\approx0,99295\)