Question

[Kim Khánh Linh]

Bài 30 (trang 116 SGK Toán 9 Tập 1)

Cho nửa đường tròn tâm $O$ có đường kính $AB$ (đường kính của một đường tròn chia đường tròn đó thành hai nửa đường tròn). Gọi $Ax$, $By$ là các tia vuông góc với $AB$ ($Ax$, $By$ và nửa đường tròn thuộc cùng một nửa mặt phẳng bờ $AB$). Qua điểm $M$ thuộc nửa đường tròn ($M$ khác $A$ và $B$), kẻ tiếp tuyến với nửa đường tròn nó cắt $Ax$ và $By$ theo thứ tự ở $C$ và $D$. Chứng minh rằng:

a) $\widehat{COD} = 90^{\circ}$.

b) $CD = AC + BD$.

c) Tích $AC.BD$ không đổi khi điểm $M$ di chuyển trên nửa đường tròn.

Answer 1

[Phạm Ngọc Quỳnh Trang]

Answer 2

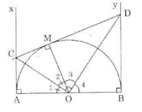
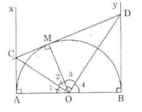
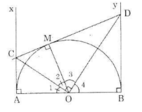
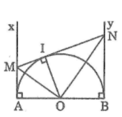
[Phương Vy]

a) $OC$ và $OD$ là các tia phân giác của hai góc kề bù $\widehat{AOM}$, $\widehat{BOM}$ nên $OC\perp OD$.

Vậy $\widehat{COD}=90^{\circ }$.

b) Theo tính chất của hai tiếp tuyến cắt nhau, ta có: $CM=AC,DM=BD$

Do đó $CD=CM+DM=AC+BD$.

c) Ta có: $AC.BD=CM.MD$

Xét tam giác $COD$ vuông tại $O$ và $OM\perp CD$ nên ta có

$CM.MD=O{M}^2=R^2$ ($R$ là bán kính của đường tròn $O$).

Vậy $AC.BD=R^2$ (không đổi).