Một vật nhỏ thực hiện dao động điều hòa theo phương trình x = 10cos(4πt -\(\dfrac{pi}{6}\)) cm. Tại thời điểm t1, vật đi qua vị trí có li độ x1= 5cm và tốc độ đang tăng. Li độ của vật ở thời điểm t2= t1- \(\dfrac{7}{48}\)s có giá trị là :
A. 9,66 cm
B. 5\(\sqrt{3}\) cm
C. -9,66 cm
D.5\(\sqrt{2}\) cm
cảm ơn mọi người đã giúp đỡ !

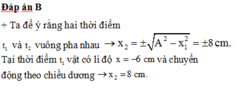

Ta có:
- Chu kì dao động: \(T=\dfrac{2\pi}{\omega}=\dfrac{2\pi}{4\pi}=0,5s\)
\(\Delta t=t_1-t_2=\dfrac{7}{48}s\)
Góc vật quét được khi từ thời điểm \(t_1\) đến \(t_2\) : \(\Delta\varphi=\omega\Delta t=4\pi.\dfrac{7}{48}=105^o\)
Tại thời điểm \(t_1\) vật đang có li độ: \(x=5\left(cm\right)=\dfrac{A}{2}\)
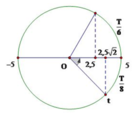
+ Với \(t_1\left(1\right)\) ta có, li độ của vật tại thời điểm \(t_1\left(2\right)\)
\(x_1=A.sin\left(15^o\right)=2,59cm\)
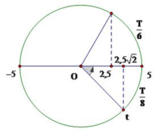
+ Với \(t_2\left(1\right)\) ta có, li độ của vật tại thời điểm \(t_2\left(2\right)\)
\(x_2=A.cos\left(15^o\right)=9,66\left(cm\right)\)\(\Rightarrow A\)