tìm số tự nhiên x thỏa mãn 5x - 7=23
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 12 2019
Đáp án cần chọn là: A
Ta có 5x−46:23=18
5x–2=18
5x=18+2
5x=20
x=20:5
x=4
Vậy x=4.
Do đó x là số chẵn.
KN
0
NT
3
S
4 tháng 3 2021
Với: y=0 thì: \(-x^2+13x=-24\text{ nên: }x^2-13x-24=0\text{ thấy ngay phương trình này ko có nghiệm nguyên}\)
\(\text{Nếu: }y>0\text{ thì: }x^2-13x=23+11^y\text{ do đó: }\left(x-1\right)^2-11x=24+11^y\text{ do đó: }\left(x-1\right)^2\text{ chia 11 dư 2}\)
THấy ngay 1 số chia 11 dư 0;+-1 ; +-2; +-3;....;+-5 mà: 0;1;4;9;16;25 không có số nào chia 11 dư 2 nên loại nên phương trình vô nghiệm
AH
Akai Haruma
Giáo viên
27 tháng 2 2021
Lời giải:
PT $\Leftrightarrow 11^y=x^2-13x-23$
Nếu $x\equiv 0\pmod 3$ thì:
$x^2-13x-23\equiv -23\equiv 1\pmod 3$
Nếu $x\equiv 1\pmod 3$ thì:
$x^2-13x-23\equiv 1-13-23\equiv 1\pmod 3$
Nếu $x\equiv 2\pmod 3$ thì:
$x^2-13x-23\equiv 1-13.2-23\equiv 0\pmod 3$
Do đó $11^y\equiv 0\pmod 3$ (vô lý) hoặc $11^y\equiv 1\pmod 3$
$\Rightarrow (-1)^y\equiv 1\pmod 3$
$\Rightarrow y$ chẵn. Đặt $y=2t$
$11^{2t}-x^2+13x+23=0$
$(2.11^{t})^2-(2x-13)^2=-261$
$(2.11^t-2x-13)(2.11^t+2x+13)=-261$
Đến đây là dạng phương trình tích cơ bản. Bạn có thể dễ dàng giải.
NN
0
TV
3
13 tháng 11 2021
a) \(\Leftrightarrow\left[{}\begin{matrix}2x+3=0\\5x-15=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\\x=3\end{matrix}\right.\)
b) \(\Leftrightarrow\left[{}\begin{matrix}3x+1=0\\3x-9=0\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\\x=3\end{matrix}\right.\)
N
13 tháng 11 2021
a. \(\left[{}\begin{matrix}2x+3=0\\5x-15=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-3}{2}\\x=3\end{matrix}\right.\)
b. \(\left[{}\begin{matrix}3x+1=0\\3x-9=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{-1}{3}\\x=3\end{matrix}\right.\)
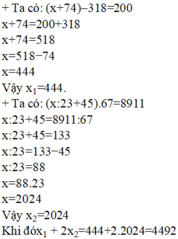
=> 5x - 7 = 8
=> 5x = 8 + 7
=> 5x = 15
=> x = 3
5x - 7 = \(2^3\)
5x - 7 = 8
5x = 8 + 7
5x = 15
x = 15 : 5
x = 3
pr hộ mình nha m.n!