Câu 4 (3,5 điểm) Cho nửa đường tròn tâm O, đường kính BC, 4 là điểm chính giữa cung BC. Dung hình bình hành ABCD. Gọi H là chân đường cao kẻ từ 4 xuống BD, E là giao điểm của BD với nửa đường tròn (O). a. Chứng minh tứ giác AHCD nội tiếp. b. Chứng minh 4OE = 2CAH c. Chứng minh DE.DB = 2.4C2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
16 tháng 1 2018
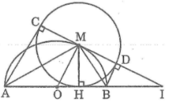
Trong đường tròn (M; MH), theo tính chất hai tiếp tuyến cắt nhau, ta có:
AC = AH và BD = BH
Khi M thay đổi trên nửa đường tròn tâm O thì AC luôn bằng AH và BD luôn bằng BH
Suy ra: AC + BD = AH + BH = AB không đổi
VH
26 tháng 3 2020
Gọi C là điểm chính giữa cung AB của nửa đường tròn tâm O đường kính AB, M là điểm bất kì trên cung BC. Kẻ CH vuông góc với AM tại H, I là giao của OH và BC, MI cắt nửa đường tròn tâm O tại D
a. CMR: CM // DB
b. Xác định vị trí của M để D,H,B thẳng hàng
c. E là giao của AD và MB. CM: EC//DM
12 tháng 2 2021
a) Xét (O) có
\(\widehat{ACB}\) là góc nội tiếp chắn \(\stackrel\frown{AB}\)
\(\stackrel\frown{AB}\) là nửa đường tròn(AB là đường kính của (O))
Do đó: \(\widehat{ACB}=90^0\)(Hệ quả góc nội tiếp)
⇔BC⊥AC tại C
⇔BC⊥AF tại C
⇔\(\widehat{BCF}=90^0\)
⇔\(\widehat{ECF}=90^0\)
Xét (O) có
\(\widehat{ADB}\) là góc nội tiếp chắn \(\stackrel\frown{AB}\)
\(\stackrel\frown{AB}\) là nửa đường tròn(AB là đường kính của (O))
Do đó: \(\widehat{ADB}=90^0\)(Hệ quả góc nội tiếp)
⇔AD⊥BD tại D
⇔AD⊥BF tại D
⇔\(\widehat{ADF}=90^0\)
⇔\(\widehat{EDF}=90^0\)
Xét tứ giác CEDF có
\(\widehat{FCE}\) và \(\widehat{FDE}\) là hai góc đối
\(\widehat{FCE}+\widehat{FDE}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: CEDF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
⇔C,E,D,F cùng nằm trên một đường tròn(đpcm)
29 tháng 5 2017
- Vì \(\Delta ADC\)nội tiếp đường tròn đường kính AO \(\Rightarrow\widehat{ADO}=90^O\Rightarrow OD⊥AC\left(1\right)\)mà \(\Delta ABC\)nội tiếp đường tròn (O) \(\Rightarrow\widehat{ACB}=90^O\Rightarrow BC⊥AC\left(2\right)\)từ 1 và 2 có \(OD\downarrow\uparrow BC\)Mà O là trung điểm BC thì D sẽ phải là trung điểm AC => AD = DC
- do \(OH⊥BC\Rightarrow\widehat{CHO}=90^0\left(3\right)\)Mà \(\widehat{ODC}=90^0\left(4\right)\)TỪ 3 và 4 có D và H nhìn OC dưới cùng một góc vuông nên DOHC nội tiếp đường tròn đường kính OC
- Vì \(OA=OB=OC=\frac{AB}{2}=3,HB=2OH\Rightarrow HB=\frac{2}{3}OB=\frac{2.3}{3}=2\).Theo hệ thức lượng trong tam giác vuông \(\Delta BCA\)có \(BC=\sqrt{HB.AB}=\sqrt{2.6}=\sqrt{12}\)Và HA=AB-HB=6-2=4 => \(AC=\sqrt{AH.AB}=\sqrt{4.6}=2\sqrt{6}\Rightarrow DC=\frac{AC}{2}=\frac{2\sqrt{6}}{2}=\sqrt{6}\)Xét Vuông \(\Delta DCB\)có:\(BD^2=DC^2+BC^2=6+12=18\),\(ID=IO=\frac{OA}{2}=\frac{3}{2}\),\(IB=IO+OB=\frac{3}{2}+3=\frac{9}{4}\)ta có :\(ID^2+BD^2=\frac{9}{4}+18=\frac{81}{4}=IB^2\)Vậy theo hệ thức lượng trong tam giác vuông có \(\Delta IDB\)Vuông tại D \(\Rightarrow ID⊥BD\)Mà ID là bán kính của (I) => BD là tiếp tuyến của (I)
