Cho hàm số y = -x2 có đồ thị (P) và A(1;1) ; B(2;0)
a) Vẽ (P)
b) Gọi d là đường thẳng đi qua B và song song với OA. Chứng minh rằng d cắt (P) tại hai điểm phân biệt C và D. Tính diện tích tam giác ACD.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

CM
3 tháng 11 2018
Đáp án A.
Phương trình hoành độ giao điểm:
x4 – 4x2 – 2 = 1 – x2 ⇔ x4 – 3x2 – 3 = 0
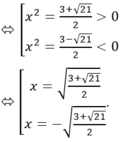

CM
30 tháng 12 2019
Đáp án C
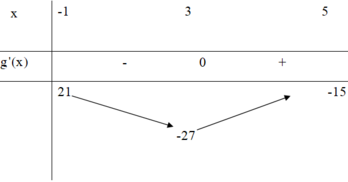
Đồ thị hàm số y = a x 2 (a ≠ 0) là một đường cong đi qua gốc tọa độ và nhận trục tung làm đối xứng.
+ Nếu a > 0 thì đồ thị nằm phía trên trục hoành.
+ Nếu a < 0 thì đồ thị nằm phía dưới trục hoành.
Trong đồ thị các hàm số đã cho; các đồ thị nằm phía dưới trục hoành là”
(1): y = -2 x 2 ; (3): y = - 3 x 2 và (4):y = -10 x 2







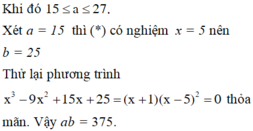
Em tự vẽ đồ thị nhé!
b. Phương trình đường thẳng OA có dạng: \(y=ax\)
Thay tọa độ của A, ta được \(a=1\)
Do \(d//OA\) nên phương trình của \(d\) có dạng: \(y=x+b\)
\(d\) đi qua B nên \(0=2+b\Rightarrow b=-2\)
Suy ra phương trình của \(d\) là: \(y=x-2\)
Phương trình hoành độ giao điểm của \(d\) và \(\left(P\right)\) là:
\(-x^2=x-2\Leftrightarrow x^2+x-2=0\left(1\right)\)
Vì a + b + c = 0 nên (1) có hai nghiệm phân biệt \(x=x_C=1,x=x_D=-2\)
\(\Rightarrow y_C=-1,y_D=-4\)
Ta có: \(x_A=x_C\Rightarrow AC\perp Ox\)
Do đó: \(S_{ACD}=\dfrac{1}{2}\left|x_C-x_D\right|.\left|y_A-y_C\right|=\dfrac{1}{2}\left(x_C-x_D\right)\left(y_A-y_C\right)=3\left(cm^2\right)\)