Trong giải cầu lông kỷ niệm ngày truyền thống học sinh sinh viên có 8 người tham gia trong đó có hai bạn Việt và Nam. Các vận động viên được chia làm hai bảng A và B, mỗi bảng gồm 4 người. Giả sử việc...

NT

Nguyễn Thùy Chi

17 tháng 5 2023

Trong giải cầu lông kỷ niệm ngày truyền thống học sinh sinh viên có 8 người tham gia trong đó có hai bạn Việt và Nam. Các vận động viên được chia làm hai bảng A và B, mỗi bảng gồm 4 người. Giả sử việc chia bảng thực hiện bằng cách bốc thăm ngẫu nhiên, tính xác suất để cả 2 bạn Việt và Nam nằm chung 1 bảng...

Đọc tiếp

#Toán lớp 11

1

NL

Nguyễn Lê Phước Thịnh

18 tháng 5 2023

\(n\left(\Omega\right)=C^4_8\cdot C^4_4\)

X: "2 bạn Việt và Nam nằm chung 1 bảng"

Số cách xếp là:

\(n\left(X\right)=C^1_2\cdot C^2_6\cdot C^4_4\)

=>P=3/7

Đúng(0)

PT

Pham Trong Bach

4 tháng 5 2017

Trong giải cầu lông kỷ niệm ngày truyền thống học sinh sinh viên có 8 người tham gia trong đó có hai bạn Việt và Nam. Các vận động viên được chia làm hai bảng A và B, mỗi bảng gồm 4 người. Giả sử việc chia bảng thực hiện bằng cách bốc thăm ngẫu nhiên. Tính xác suất để cả hai bạn Việt và Nam nằm chung một bảng đấu. A. B. C. ...

Đọc tiếp

#Toán lớp 11

1

CM

Cao Minh Tâm

4 tháng 5 2017

Đáp án B

Số phần tử của không gian mẫu là:

Gọi X là biến cố “cả hai bạn Việt và Nam nằm chung một bảng đấu’

Số kết quả thuận lợi cho biến cố X là:

Vậy xác suất cần tính

Đúng(0)

PT

Pham Trong Bach

16 tháng 9 2017

Trong giải cầu lông kỷ niệm ngày truyền thống học sinh sinh viên có 8 người tham gia trong đó có hai bạn Việt và Nam. Các vận động viên được chia làm hai bảng A và B, mỗi bảng gồm 4 người. Giả sử việc chia bảng thực hiện bằng cách bốc thăm ngẫu nhiên. Tính xác suất để cả hai bạn Việt và Nam nằm chung một bảng đấu. A. 3 5 B. 3 7 C. 3 11 D. ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

16 tháng 9 2017

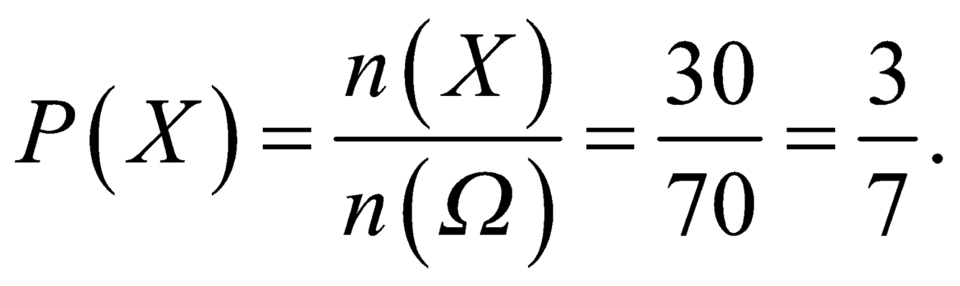
Số phần tử của không gian mẫu là: n Ω = C 8 4 = 70

Gọi X là biến cố: “cả hai bạn Việt và Nam nằm chung một bảng đấu’

Số kết quả thuận lợi cho biến cố X là: n X = C 2 1 C 2 6 = 30

Vậy xác suất cần tính P X = n X n Ω = 30 70 = 3 7

Đáp án B

Đúng(0)

PT

Pham Trong Bach

19 tháng 12 2017

Giải bóng truyền quốc tế VTV Cup có 8 đội tham gia, trong đó có hai đội Việt Nam. Ban tổ chức bốc thăm ngẫu nhiên để chia thành hai bảng đấu, mỗi bảng 4 đội. Xác suất để hai đội của Việt Nam nằm trong hai bảng khác nhau bằng A. 2 7 B. 5 7 C. 3 7 D. 4 7 ...

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

19 tháng 12 2017

Số cách chia 8 đội thành 2 bảng là:

Gọi A là biến cố: “Hai đội của Việt Nam được xếp vào 2 bảng khác nhau”.

Số các chia 2 đội của Việt Nam vào 2 đội là:

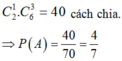
Chọn D.

Đúng(0)

PT

Pham Trong Bach

3 tháng 10 2019

Đoàn trường THPT Nguyễn Đình Liễn tổ chức giao lưu bóng chuyền học sinh giữa các lớp nhân dịp chào mừng ngày 26/3. Sau quá trình đăng kí có 10 đội tham gia thi đấu từ 10 lớp, trong đó có lớp 10A1 và 10A2. Các đội chia làm hai bảng, kí hiệu là bảng A và bảng B, mỗi bảng 5 đội. Việc chia bảng được thực hiện bằng cách bốc thăm ngẫu nhiên. Tính xác suất để 2 đội 10A1 và 10A2 thuộc hai...

Đọc tiếp

#Toán lớp 11

1

CM

Cao Minh Tâm

3 tháng 10 2019

Chọn A

+ Chia đều 10 đội vào 2 bảng A và B có cách.

Do đó số phần tử của không gian mẫu là :

+ Sắp xếp đội của lớp 10A1 và 10A2 vào 2 bảng khác nhau A và B có 2! cách.

Chọn 4 đội trong 8 đội còn lại để xếp vào bảng có đội lớp 10A1 có C 8 4 cách.

Bốn đội còn lại xếp vào bảng còn lại.

Suy ra số cách chia đều 10 đội vào 2 bảng sao cho 2 đội 10A1 và 10A2 nằm ở 2 bảng khác nhau là

Gọi A là biến cố “Chia đều 10 đội vào 2 bảng sao cho 2 đội 10A1 và 10A2 nằm ở 2 bảng khác nhau ” thì số các kết quả thuận lợi cho biến cố A là:

+ Xác suất cần tìm là: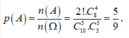

Đúng(0)

3T

33-Thành-9D

10 tháng 4 2022

1 trường tổ chức cho 330 người gồm giáo viên và học sinh đi tham quan Dinh Độc Lập.Biết giá vé tham quan tòa nhà chính Di tích lịch sử Dinh Độc Lập của mỗi giáo viên là 40 000 đồng,của mỗi học sinh là 20 000 đồng. Nhân dịp kỷ niệm 90 năm Ngày thành lập Đoàn TNCS Hồ Chí Minh (26/3/1931-26/3/2021) nên được giảm 10% cho mỗi vé vào tham quan,vì vậy mà nhà trường chi phải trả số tiền là 6 480 000 đồng.Hỏi có bao...

Đọc tiếp

#Toán lớp 9

1

N

nthv_.

10 tháng 4 2022

Gọi x, y (người) lần lượt là số giáo viên và học sinh của trường \(\left(x,y\in N\circledast\right)\)

Vì trường tổ chức cho 330 người gồm giáo viên và học sinh đi tham quan Dinh Độc Lập nên: \(x+y=330_{\left(1\right)}\)

Vì nhân dịp kỷ niệm 90 năm Ngày thành lập Đoàn TNCS Hồ Chí Minh (26/3/1931 - 26/3/2021) do đó được giảm 10% cho mỗi vé vào tham quan và nhà trường chi phải trả số tiền là 6 480 000 đồng biết mối vé giáo viên là 40 000 đồng còn học sinh là 20 000 đồng, nên:

\(x\cdot40000\left(100\%-10\%\right)+y\cdot20000\left(100\%-10\%\right)=6480000_{\left(2\right)}\)

Từ (1) và (2), ta có hpt: \(\left\{{}\begin{matrix}x+y=330\\x\cdot40000\left(100\%-10\%\right)+y\cdot20000\left(100\%-10\%\right)=6480000\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=30\\y=300\end{matrix}\right.\)

Vậy có 30 giáo viên và 300 học sinh

Đúng(2)

AB

Anh Bùi Quang

10 tháng 7 2016 - olm

Bài 1:2 người thợ làm chung một công việc thì phải làm trong 7 giờ mới xong. Nhưng người thợ cả chỉ làm 4 giờ rồi nghỉ do đó người thứ hai phải làm 9 giờ nữa mới xong.Hỏi nếu làm riêng thì mỗi người phải làm mấy giờ mới xong? Bài 2: Hai người cùng làm một công việc trong 16 giờ thì xong . Nếu người thứ nhất làm trong 3 giờ, người thứ hai làm trong 6 giờ thì họ làm 25% công việc....

Đọc tiếp

Bài 1:
2 người thợ làm chung một công việc thì phải làm trong 7 giờ mới xong. Nhưng người thợ cả chỉ làm 4 giờ rồi nghỉ do đó người thứ hai phải làm 9 giờ nữa mới xong.Hỏi nếu làm riêng thì mỗi người phải làm mấy giờ mới xong?

Bài 2:
Hai người cùng làm một công việc trong 16 giờ thì xong . Nếu người thứ nhất làm trong 3 giờ, người thứ hai làm trong 6 giờ thì họ làm 25% công việc. Hỏi mỗi người làm công việc đó một mình thì trong bao lâu sẽ hoàn thành công việc đó?

Bài 3: Một quầy bán hàng có 48 gói kẹo gồm loại 0,5kg; loại 0,2kg và loại 0,1kg. Khối lượng cả 48 gói la 9kg. Hỏi mỗi loại có bao nhiêu gói (biết số gói 0,1kg gấp 3 lần số gói 0,2kg)

Có một số dầu hỏa, nếu đổ vào các can 6 lít thì vừa hết. nếu đổ vào các can 10 lít thì thừa 2 lít và số can giảm đi 5can. Hỏi có bao nhiêu lít dầu?

Bài 5:
Cô giáo đem chia một số kẹo cho các em. Cô nhẩm tính, nếu chia cho mỗi em 5 chiếc thì thừa 3 chiếc, nếu chia cho mỗi em 6 chiếc thì thiếu 5 chiếc. Hỏi cô giáo có bao nhiêu cái kẹo ?

Bài 6:
Có 145 tờ tiền mệnh giá 5000đ, 2000đ và 1000đ. Số tiền của 145 tờ tiền giấy trên là 312 000đ. Số tiền loại mệnh giá 2000đ gấp đôi loại 1000đ. Hỏi mỗi loại tiền có mấy tờ.

Bài 7:
Bác Toàn mua 5 cái bàn và 7 cái ghế với tổng tiền phải trả là 3 010 000 đồng . Giá 1 cái bàn đắt hơn 1 cái ghế 170 000 đồng. Nếu mua 1 cái bàn và 2 cái ghế thì hết bao nhiêu tiền?

Bài 8:
Một nhóm học sinh lớp 4 tham gia sinh hoạt ngoại khóa được chia thành các tổ để sinh hoạt.Nếu mỗi tổ 6 nam và 6 nữ thì thừa 20 bạn nam .Nếu mỗi tổ 7 nam và 5 nữ thì thừa 20 nữ . Hỏi có bao nhiêu nam ,bao nhiêu nữ?

Bài 9:
Có một số l dầu và một số can. Nếu mỗi can chứa 5 l dầu thì còn thừa 5 l; nếu mỗi can chứa 6 l dầu thì có một can để không. Hỏi có bao nhiêu can, bao nhiêu l dầu?

Bài 10:
Nhà trưòng giao cho một số lớp trồng cả hai loại cây là cây thông và cây bạch đàn. Số lượng cây cả hai loại đều bằng nhau. Thầy Hiệu phó tính rằng: nếu mỗi lớp trồng 35 cây thông thì còn thừa 20 cây thông; nếu mỗi lớp trồng 40 cây bạch đàn thì còn thiếu 20 cây bạch đàn. Hỏi nhà trường đã giao tất cả bao nhiêu cây thông và cây bạch đàn cho mấy lớp đem trồng, biết toàn bộ số cây đó đã được trồng hết.

Bài 11:
Tổng hai số bằng 104. Tìm hai số đó biết rằng 1/4 số thứ nhất kém 1/6 số thứ hai là 4 đơn vị.

Bài 13:
Một vận động viên bắn súng trong một lần tập huấn phải bắn tất cả 50 viên đạn. Mỗi viên trúng đích được cộng 10 điểm, mỗi viên trượt đích bị trừ 5 điểm. Sau khi bắn hết 50 viên đạn vận động viên đó đạt được 440 điểm. Hỏi vận động viên đó bắn trúng đích bao nhiêu viên?

Bài 14:
Để chuẩn bị cho kì thi học sinh giỏi .Một học sịnh phải giải 40 bài toán. Biết 1 bài đạt loại giỏi được cộng 20 điểm, mỗi bài khá hay trung bình được cộng 5 điểm, 1 bài yếu kém trứ bớt đi 10 điểm. Làm xong 40 bài học sinh đó được tổng điểm là 155 điểm. Hỏi em làm được bao nhiêu bài bài loại giỏi, yếu kém. Biết số bài khá và trung bình là 13 bài.

#Toán lớp 4

0

LB

Lê Bảo Trân

25 tháng 4 2021 - olm

Trong giải chạy Edurun 2021, Hệ thống giáo dục Vinschool đã thu hút được đông đảo thí sinh tham gia, bao gồm học sinh, phụ huynh và cán bộ nhân viên. Trong đó, số lượng học sinh tham gia là 600 HS chiếm 40% tổng số người tham gia. Số lượng PH tham gia chiếm 13/30 tổng số người tham gia. Còn lại là số cán bộ nhân viên. Hỏi có tất cả bao nhiêu người thi chạy? Số lượng mỗi nhóm PH, cán bộ nhân...

Đọc tiếp

#Toán lớp 6

1

VK

Vũ Khôi Nguyên

25 tháng 4 2021

Có tất cả số người thi chạy là:

600 : 40 x 100 = 1500 ( người)

Số PH thi chạy là:

1500 x 13/30 = 650 ( PH)

Số cán bộ viên là:

1500 - ( 600 + 650 ) = 250 ( người)

Đ/s: .........

Đúng(0)

TH

Tùng hà 0000000

29 tháng 11 2021

hướng tới kỉ niệm ngày truyền thống học sinh, sinh viên (9/1/2020).thầy tổng phụ trách phát động phong trào thi đua trong đó có nội dung xây dựng tình bạn trong sáng lành mạnh. Là một học sinh của trường em sẽ làm j để hưởng ứng hoạt động này?

các bạn giúp mình vs

#Giáo dục công dân lớp 8

0

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP