Cho hàm số y=-1/2x^2
a)Khảo sát và vẽ đồ thị (P) của hàm số trên
b)Lập phương trình đường thẵng ( d) đi qua A(-2;-2) và tiếp xúc với (P)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b.
y = x^4 + 2(m + 1)x^2 + 1
y' = 4x^3 + 4(m + 1)x
y'= 0=> x=0 và x^2 + (m + 1)= 0 (*)
để đồ thị hàm số có 3 điểm cực trị thì (*) có 2 nghiệm phân biệt
=> m+1<0
<=> m< -1
ta có:
y= [4x^3 + 4(m + 1)x]*x/4+ (m+1)x^2+ 1
y= y'*x/4+ (m+1)x^2+ 1
đường cong đi qua các điểm cực trị thỏa mãn y'= 0
=> pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
Vậy để đồ thị hàm số có 3 điểm cực trị thì m< -1
và pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
b.
y = x^4 + 2(m + 1)x^2 + 1
y' = 4x^3 + 4(m + 1)x
y'= 0=> x=0 và x^2 + (m + 1)= 0 (*)
để đồ thị hàm số có 3 điểm cực trị thì (*) có 2 nghiệm phân biệt
=> m+1<0
<=> m< -1
ta có:
y= [4x^3 + 4(m + 1)x]*x/4+ (m+1)x^2+ 1
y= y'*x/4+ (m+1)x^2+ 1
đường cong đi qua các điểm cực trị thỏa mãn y'= 0
=> pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
Vậy để đồ thị hàm số có 3 điểm cực trị thì m< -1
và pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1

Câu 2:
a) Để đồ thị hàm số \(y=\left(m+1\right)x^2\) đi qua điểm A(1;2) thì
Thay x=1 và y=2 vào hàm số \(y=\left(m+1\right)x^2\), ta được:
m+1=2
hay m=1
Vậy: m=1

a) (P) là parabol đi qua gốc toạ độ O(0; 0) ; điểm (1; 1/2) và điểm (-1;1/2)
b) A \(\in\) (P) => yA = \(\frac{1}{2}\). xA2 = \(\frac{1}{2}\). (-1)2 = \(\frac{1}{2}\)=> A (-1; \(\frac{1}{2}\))
B \(\in\) (P) => yB = \(\frac{1}{2}\).xB2 = \(\frac{1}{2}\).4 = 2 => B (2; 2)
+) đường thẳng có hệ số góc bằng \(\frac{1}{2}\) có dạng y = \(\frac{1}{2}\)x + b (d)
A \(\in\) d => yA = \(\frac{1}{2}\).xA + b => \(\frac{1}{2}\) = \(\frac{1}{2}\). (-1) + b => b = 1
Vậy đường thẳng (d) có dạng y = \(\frac{1}{2}\)x + 1
Nhận xét: yB = \(\frac{1}{2}\).xB + 1 => B \(\in\) (d)

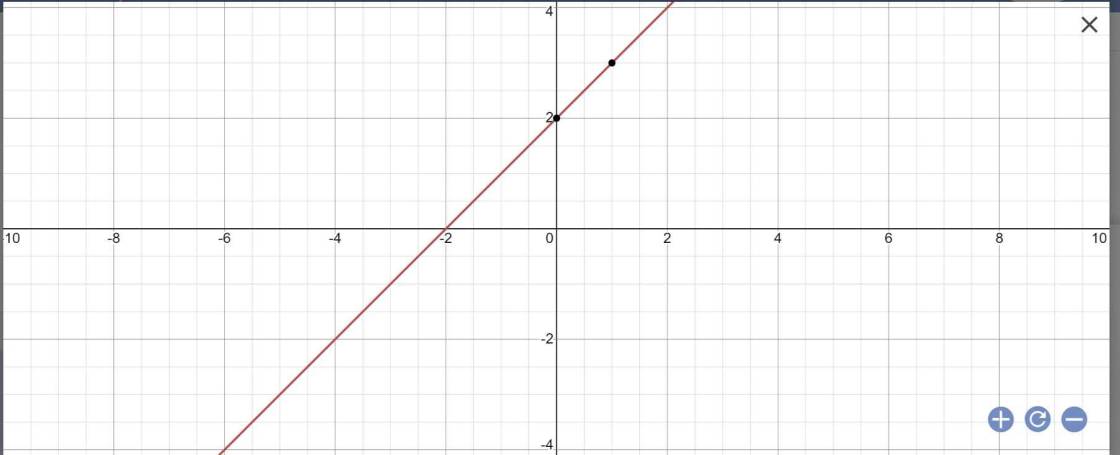
b: Tọa độ giao điểm là:
2x-1=x+2 và y=x+2
=>3x=3 và y=x+2
=>x=1 và y=3
a: