Giải dùm đi đang thi
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 1 2018
A = 51 + 52 + ... + 51999+ 52000
A = ( 51 + 52 ) + ... + ( 51999 + 52000 )
A = 51 . ( 1 + 5 ) + ... + 51999 . ( 1 + 5 )
A = 51 . 6 + ... + 51999 . 6 = 6 . ( 51 + ... + 51999 ) \(⋮\)6
Vậy A \(⋮\)6
4 tháng 1 2018
A = 51 + 52 + 53................... + 52000 chia hết cho 6
A = ( 51 + 52 ) +...................+ ( 51999 + 52000 )
A = ( 5.1 + 5. 5 ) +...................+ ( 51999. 1 + 51999. 5 )
A = ( 5. 1 + 5 ) +.....................+ ( 51999. 1 + 5 )
A = ( 5. 6 ) +....................+ ( 51999. 6 )
Vì ( 5. 6 ) +....................+ ( 51999. 6 ) chia hết cho 6
Nên A chia hết cho 6
NV
1
A
17 tháng 10 2021
Bài 1:
a) Ta có:
\(a=\dfrac{v-v_0}{t-t_0}=\dfrac{10-50}{20}=-2\) (m/\(s^2\))
=> PTCĐ: \(x=x_0+v_0t+\dfrac{1}{2}at^2\)
\(\Leftrightarrow\) \(x=50t+\dfrac{1}{2}.\left(-2\right).t^2\)
\(\Leftrightarrow\) \(x=50t-t^2\)
b) Quảng đường vật đi được:
\(S=v_0+\dfrac{1}{2}at^2\)\(=50.20+\dfrac{1}{2}.\left(-2\right).20^2=600\) (m)
H9
HT.Phong (9A5)
CTVHS
26 tháng 3 2023
\(s=0,8km=800m\)
\(t=30p=1800s\)
a. Công sinh ra là:
\(A=F.s=1000.800=800000J\)
b. Công suất của ngựa:
\(\text{℘ }=\dfrac{A}{t}=\dfrac{800000}{1800}\approx444,4W\)
C
26 tháng 3 2023
Tóm tắt:
\(F=1000N\\ s=0,8km\\ =800m\\ t=30min\\ =1800s\\ ----------\\ A/A=?J\\ B/P\left(hoa\right)=?W\)
Giải:
A/ Công sinh ra khi con ngựa đi trên đường đó: \(A=F.s\\ =1000.800=800000\left(J\right)\)
B/ Công suất của con ngựa: \(P\left(hoa\right)=\dfrac{A}{t}\\ =\dfrac{800000}{1800}\approx444,44\left(W\right).\)
DH
4 tháng 5 2016
Khi trồng chuối( hoặc trồng mía)người ta phải phạt bớt lá để giảm bớt sự bay hơi,làm cây ít bị mất nước(do lúc mới trồng chuối rễ chuối còn chưa phát triển khỏe mạnh nên ko thể hút nước được)
PT
4 tháng 5 2016
Khi trồng chuối hay trồng mía người ta phải phạt bớt lá là để giảm sự thoát hơi nước qua bề mặt lá làm cho cây đỡ mất nước và cây có thể sống sau khi trồng.
23 tháng 1 2022
a: Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
=>\(\widehat{ACB}=30^0\)
\(\Leftrightarrow\widehat{ABC}=60^0\)
b: \(AC=6\sqrt{3}\left(cm\right)\)
\(C=AB+AC+BC=6+12+6\sqrt{3}=18+6\sqrt{3}\left(cm\right)\)
\(S=\dfrac{6\sqrt{3}\cdot6}{2}=18\sqrt{3}\left(cm^2\right)\)
c: Xét (O) có
MA là tiếp tuyến
MC là tiếp tuyến
Do đó: MA=MC
hay M nằm trên đường trung trực của AC(1)
Ta có: OA=OC
nên O nằm trên đường trung trực của AC(2)
Từ (1) và (2) suy ra OM là đường trung trực của AC
hay OM\(\perp\)AC
HQ
2
11 tháng 5 2023
Ta có:
n - 1
------ ∈ ℤ
n + 3
Khi đó, ta có thể viết n - 1 dưới dạng (n + 3)k + r, với k là số nguyên và 0 ≤ r < n + 3.
Vì n - 1 < n + 3, n - (n + 3) < 1, suy ra r = n - 1.
Thay r = n - 1 vào phương trình ban đầu, ta được:
n - 1
------ = k
n + 3
n - 1 = k(n + 3)
n - kn = 3k + 1
n(1 - k) = 3k + 1
Ta thấy rằng 1 - k không thể âm, vì nếu như vậy thì n sẽ âm, điều này không đúng vì n thuộc N.
Nếu 1 - k = 1, ta có n = 4.
Nếu 1 - k > 1, ta có:
n = (3k + 1)/(1 - k)
Do đó, 1 - k phải chia hết cho 3k + 1 để n là số nguyên dương.
Ta thử với k = 1, 2, 3,… và tính giá trị tương ứng của 1 - k. Khi đó, ta được:
k1 - k| 1 | 0 |
| 2 | -1 |
| 3 | -2 |
| 4 | -3 |
| 5 | -4 |
| 6 | -5 |
Ta thấy rằng 3k + 1 không chia hết cho 1 - k với bất kỳ giá trị k nào lớn hơn 1. Do đó, n = 4 là duy nhất.
Vậy n = 4 là giá trị nguyên dương thỏa mãn yêu cầu của bài toán.
- Khi treo quả cân có khối lượng 50g thì lò xo dãn 2 cm
=> Khi treo 2 quả cân có khối lượng 50 g thì lò xo dãn 2+2=4cm
Vì độ dãn của lò xo tỉ lệ thuận với khối lượng của vật treo do đó khi treo 2 quả cân có khối lượng 50 g thì lò xo dãn ra một đoạn là: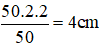
Tạch r