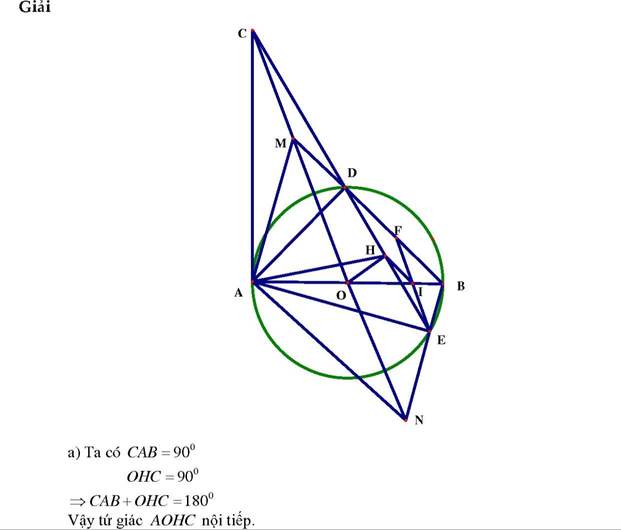
Cho đường tròn (O) đường kính AB=2R .Từ A vẽ tiếp tuyến Ax với (O) (A là tiếp điểm ). Trên tia Ax lấy điểm C sao cho AC =2R .Qua C vẽ đường thẳng cắt đường tròn ( O) tại hai điểm D và E ( d nằm giữa C và E ; đường thẳng này cũng cắt đoạn thẳng OB ) Gọi H là trung điểm đoạn thẳng DE
a) Chứng minh CA2 =CD.CE
b) Chứng minh : tứ giác AOCH nội tiếp
c) Đoạn thẳng CB cắt đường tròn (O) tại K .Tính số đo góc AOK và diện tích hình quạt AOK theo R và 'pi"
d) ĐƯờng thẳng CO cắt tia BD , tia BE lần lượt tại M và N .Chứng minh O là trung điểm đoạn thẳng MN
(CHỈ CẦN CÂU D THÔI Ạ )