Cho tam giác ABC nhọn (AB < AC) có 3 đường cao AE, BD, CK cắt nhau tại Ha. Chứng minh tam giác HKB đồng dạng tam giác HDC và CE.CB = CD.CAb. Gọi S là giao điểm của 2 đường thẳng DK và BC . Chứng minh...

DD

Đào Đức Dương

6 tháng 5 2023

Cho tam giác ABC nhọn (AB < AC) có 3 đường cao AE, BD, CK cắt nhau tại Ha. Chứng minh tam giác HKB đồng dạng tam giác HDC và CE.CB = CD.CAb. Gọi S là giao điểm của 2 đường thẳng DK và BC . Chứng minh góc SBK= góc SDCc. Gọi O là giao điểm của BD và KE. Từ O kẻ đường thẳng // với đường thẳng KD, đường thẳng này cắt AC tại I. Gọi M là giao điểm của EI và KD. Chứng minh DK=DMGiúp mình câu C...

Đọc tiếp

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

9 tháng 5 2023

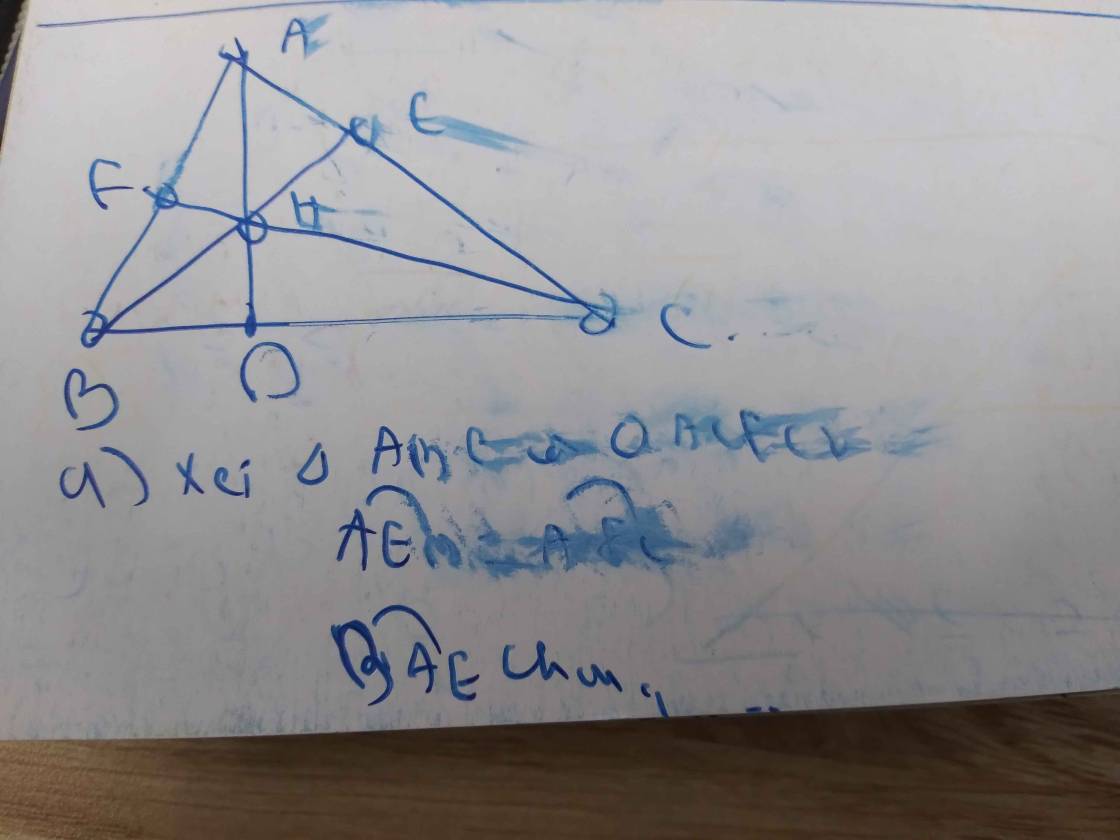
a: Xét ΔHKB vuông tại K và ΔHDC vuông tại D có

góc KHB=góc DHC

=>ΔKHB đồng dạng với ΔDHC

Xet ΔCDB vuông tại D và ΔCEA vuông tại E có

góc C chung

=>ΔCDB đồng dạng với ΔCEA

=>CD/CE=CB/CA

=>CD*CA=CE*CB

b: góc BKC=góc BDC=90 độ

=>BKDC nội tiếp

=>góc SBK=góc SDC

Đúng(0)

BP

Bích Phượng My

23 tháng 2 2022

Cho tam giác ABC nhọn có AB bé hơn AC các đường cao BD, CE cắt nhau tại H. 1) chứng minh AE x AB = AC x AD 2) chứng minh tam giác ADE đồng dạng với tam giác ABC 3) gọi M, N là giao điểm của DE và AH và DC. Chứng minh MD x NE = ME x ND

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

23 tháng 2 2022

1: Xét ΔABD vuông tại D và ΔACE vuông tại E có

\(\widehat{A}\) chung

Do đó: ΔABD∼ΔACE

Suy ra: AB/AC=AD/AE
hay \(AB\cdot AE=AC\cdot AD\)

2: Xét ΔADE và ΔABC có

AD/AB=AE/AC

\(\widehat{DAE}\) chung

Do đó:ΔADE∼ΔABC

Đúng(0)

G

gffhgfv

10 tháng 5 2022 - olm

cho tam giác nhọn ABC (AB<AC) có đường cao BE , CF cắt nhau tại H .a) chứng minh tam giác FHB và tam giác EAB đồng dạng . b) chứng minh AF.AB = AE .AC . c) đường thẳng qua B và song song với È cắt AC tại M . gọi I là trung điểm BM , D là giao điểm EI và BC . chứng minh A H D thẳng hàng

#Toán lớp 8

0

LX

Lưu Xuân Hưởng

7 tháng 5 2015 - olm

Cho tam giác ABC có ba góc nhọn (AB<AC), hai đường cao BD và CE cắt nhau tại H.

1. Chứng minh tam giác ABD đồng dạng tam giác ACE, từ đó suy ra AB. AE = AC.AD

2. Chứng minh tam giác ADE đồng dạng tam giác ABC

3. Gọi I là giao điểm của DE và CB và M là trung điểm của BC. Chứng minh ID.IE=IM²-MC²

4. Biết BC=15. Tính P = BH.BD + CH.CE

#Toán lớp 8

2

LX

Lưu Xuân Hưởng

7 tháng 5 2015

ĐÁP ÁN BÀI HÌNH CÂU 3, 4 ĐỀ THI TOÁN 8 KỲ 2 TINH BẮC NINH NĂM HỌC 2014-2015

3. Từ ID.IE=IM²-MC²= ( IM - MC ) ( IM + MC ) = IB. IC ( vì MB = MC ). Xét tam giác IDB và tam giác IEC có góc I chung, góc IDB = góc ICE ( vì phụ với hai góc bằng nhau góc ADE = góc ABC theo câu 2). suy ra tam giác IBD đồng dạng tam giác IEC(g-g). suy ra ID/IC = IB/IIE => ID.IE = IB.IC hay ID.IE=IM²-MC^2.(đpcm).

4. Hạ đường cao AH cắt BC tại K. Chứng minh được tam giác BHK đồng dạng tam giác BCD và tam giác CHK đồng dạng tam giác CBE (g-g). Suy ra BH. BD = BC. BK và CH.CE = BC. CK => P = BH.BD + CH.CE = BC ( BK+CK ) = BC. BC= BC²

Thay BC = 15 vào biểu thức ta được P = BH.BD + CH.CE = 15²= 225.

Đúng(1)

NA

Na Akino

7 tháng 5 2016

giải câu 1 với câu 2 giùm em với

Đúng(0)

S

studyinclass

20 tháng 4 2023

Cho tam giác nhọn ABC (AB<AC), các đường cao AD,BE và CF cắt nhau tại H.

a) Chứng minh rằng: Tam giác ABC đồng dạng tam giác ACF và AB.AF = AC.AE

b) Chứng minh rằng: góc AED = góc ACB

c) Gọi M là trung điểm của BC, K là giao điểm của đường thẳng EF và đường thẳng BC. Chứng minh BC² = 4.MD.MK

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

20 tháng 4 2023

loading...

Đúng(0)

NT

Nguyễn Tiến Thanh

19 tháng 3 2021

Cho tam giác ABC nhọn hai đường cao BD và CE cắt nhau tại H.

a) Chứng minh tam giác ABD đồng dạng tam giác ACE

b) Chứng minh BH.HD = CH.HE

c) Chứng minh Chứng tam giác ADE đồng dạng tam giác ABC

d) Gọi F là giao điểm của AH và BC, K là trung điểm của AH. Chứng minh: BF.CF = KF² – HD²

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

19 tháng 3 2021

a) Xét ΔABD vuông tại D và ΔACE vuông tại E có

\(\widehat{BAD}\) chung

Do đó: ΔABD∼ΔACE(g-g)

b) Xét ΔEHB vuông tại E và ΔDHC vuông tại D có

\(\widehat{EHB}=\widehat{DHC}\)(hai góc đối đỉnh)

Do đó: ΔEHB∼ΔDHC(g-g)

Suy ra: \(\dfrac{HE}{HD}=\dfrac{HB}{HC}\)(Các cặp cạnh tương ứng tỉ lệ)

hay \(BH\cdot HD=CH\cdot HE\)(đpcm)

Đúng(0)

HX

ha xuan duong

8 tháng 5 2023

cho tam giác ABC có 3 góc nhọn, các đường cao BD và CE cắt nhau tại H a, CM tam giác ABD đồng dạng với tam giác ACE
b, chứng minh góc ADE = góc ABC
c, gọi K là giao điểm của AH và BC, F là giao điểm của DK và HC cm HE.CF=CE.HF
giúp phần c vs ạ

#Toán lớp 8

1

NL

Nguyễn Lê Phước Thịnh

9 tháng 5 2023

a: Xét ΔABD vuông tại D và ΔACE vuông tại E có

góc A chung

=>ΔABD đồng dạng với ΔACE

b: ΔABD đồng dạng với ΔACE
=>AD/AE=AB/AC

=>AD/AB=AE/AC
=>ΔADE đồng dạng với ΔABC

=>góc ADE=góc ABC

Đúng(1)

A

anh

23 tháng 3 2021

Cho tam giác ABC nhọn (AB < AC) có hai đường cao AD và BE cắt nhau tại H. a) Chứng minh tam giác HEA đồng dạng tam giác HDB. b) Kẻ DK vuông góc AC tại K. Chứng minh CD2 = CK.CA c) Gọi N là trung điểm của CK. Trên tia đối của tia AD lấy điểm F sao cho AF = AD. Chứng minh FK vuông góc DN tại S.

#Toán lớp 8

1