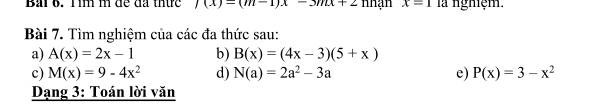
Cần gấp bài 7 ạ!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
các bạn giúp mình bài 7, bài 8, bài 9 nhé. cần gấp ạ
15 tháng 8 2021
Câu 7 :
a, Tham khảo : https://olm.vn/hoi-dap/detail/43902845942.html
b, Tham khảo : https://olm.vn/hoi-dap/detail/7963533510.html
10 tháng 10 2021
Bài 6:
a: \(\sqrt{\dfrac{2}{3-\sqrt{5}}}=\dfrac{\sqrt[4]{2}\cdot\left(\sqrt[2]{5}+1\right)}{2}\)
b: \(\sqrt{\dfrac{a-4}{2\left(\sqrt{a}-2\right)}}=\dfrac{\sqrt{2}\left(\sqrt{a}+2\right)}{2}\)
12 tháng 7 2021
Bài 8:
a) Ta có: AD+DB=AB(D nằm giữa A và B)
AE+EC=AC(E nằm giữa A và C)
mà DB=EC(gt)
và AB=AC(ΔABC cân tại A)
nên AD=AE
Xét ΔADE có AD=AE(cmt)
nên ΔADE cân tại A(Định nghĩa tam giác cân)
b) Xét ΔABC có
\(\dfrac{AD}{AB}=\dfrac{AE}{AC}\left(AD=AE;AB=AC\right)\)
Do đó: DE//BC(Định lí Ta lét đảo)
c) Xét tứ giác BDEC có DE//BC(cmt)
nên BDEC là hình thang có hai đáy là DE và BC(Định nghĩa hình thang)
Hình thang BDEC(DE//BC) có \(\widehat{B}=\widehat{C}\)(hai góc ở đáy của ΔABC cân tại A)
nên BDEC là hình thang cân(Dấu hiệu nhận biết hình thang cân)
12 tháng 7 2021
Bài 7:
a) Xét ΔADE vuông tại E và ΔBCF vuông tại F có
AD=BC(ABCD là hình thang cân)
\(\widehat{B}=\widehat{C}\)(ABCD là hình thang cân)
Do đó: ΔADE=ΔBCF(Cạnh huyền-góc nhọn)
Suy ra: DE=CF(Hai cạnh tương ứng)
\(\Leftrightarrow DE+EF=CF+FE\)
\(\Leftrightarrow DF=CE\)
b) Xét tứ giác ABFE có
AE//BF(gt)
AE=BF(ΔAED=ΔBFC)
Do đó: ABFE là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Suy ra: AB=EF(Hai cạnh đối)
NL
1
17 tháng 10 2021
Bài 7:
a: \(A=x+\sqrt{x}\ge0\forall x\)
Dấu '=' xảy ra khi x=0
0P
0
GM
0
NT
23
10 tháng 7 2021
-5/7.2/11+-5/7.9/11+5/7
=-5/7 . (2/11+9/11+5/7)
=-5/7.12/7
=-60/7
10 tháng 7 2021
-5/7 . 2/11 + (-5/7) . 9/11 + 5/7
= -5/7 . 2/11 + -5/7 . 9/11 + (-5/7) . (-1)
= (-5/7) . (2/11 + 9/11 -1)
= (-5/7) . 0
=0
ks nha bạn
LR
3
TG
31 tháng 1 2021
\(-2\left(2x-7\right)^2=2\)
\(\Rightarrow\left(2x-7\right)^2=-4\)
Mà: \(\left(2x-7\right)^2\ge0\)
=> Ko có giá trị x cần tìm
a: A(x)=0
=>2x-1=0
=>x=1/2
b: B(x)=0
=>(4x-3)(x+5)=0
=>x=3/4 hoặc x=-5
c: P(x)=0
=>3-x^2=0
=>x^2=3
=>\(x=\pm\sqrt{3}\)
d: M(x)=0
=>9-4x^2=0
=>4x^2=9
=>x=3/2 hoặc x=-3/2
e: N(a)=0
=>2a^2-3a=0
=>a=0; a=3/2