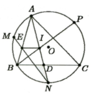
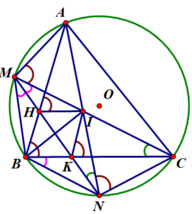
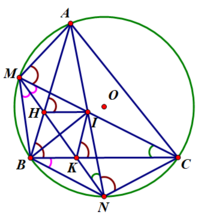
Cho đường tròn (O) lấy 3 điểm A,B, theo thứ tự gọi M,N,P lần lượt là điểm chính giữa của các cung AB,BC,CA. BP cắt AN tại I , MN cắt AB tại E .
a/ chứng minh tam giác BNI cân .
b/ chứng minh AE.BN=EB.AN
c/ chứng minh EI // BC.
d/ Gọi D là giao điểm của AN và BC . Chứng minh AN/BN = AB/BD