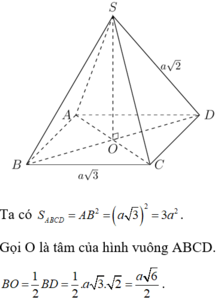
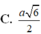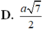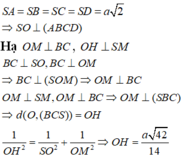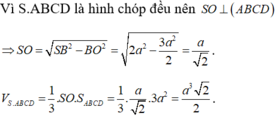Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, SA = SB = SC = SD = a sqrt(3). Tính khoảng cách từ tâm O của hình vuông ABCD đến mặt bên (SBC)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B
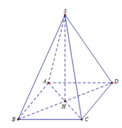
Ta có: 2 B H 2 = a 3 2 ⇒ B H 2 = 3 a 2 2
S H = S B 2 − B H 2 = 2 a 2 − 3 a 2 2 = a 2
Thể tích khối chóp S.ABCD là:
V = 1 3 . S H . S A B C D = 1 3 . a 2 . a 3 2 = a 3 2

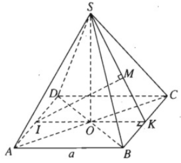
a) Gọi O là tâm hình vuông ABCD , dễ thấy I, O, K thẳng hàng. Vì K là trung điểm của BC nên SK ⊥ BC.
Ta có 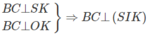
Do đó (SBC) ⊥ (SIK)
b) Hai đường thẳng AD và SB chéo nhau. Ta có mặt phẳng (SBC) chứa SB và song song với AD. Do đó khoảng cách giữa AD và SB bằng khoảng cách giữa AD và mặt phẳng (SBC).
Theo câu a) ta có (SIK) ⊥ (SBC) theo giao tuyến SK và khoảng cách cần tìm là IM, trong đó M là chân đường vuông góc hạ từ I tới SK. Dựa vào hệ thức IM. SK = SO. IK
ta có 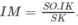
Ta lại có:
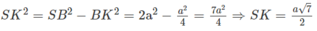
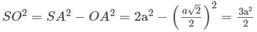
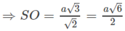
Do đó:
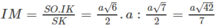
Vậy khoảng cách giữa hai đường thẳng AD và SB là bằng 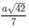

\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\BD\perp AC\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
Từ A kẻ \(AH\perp SO\Rightarrow AH\perp\left(SBD\right)\)
\(\Rightarrow AH=d\left(A;\left(SBD\right)\right)\)
\(AC=a\sqrt{2}\Rightarrow AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\)
Hệ thức lượng: \(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AO^2}\Rightarrow AH=\dfrac{SA.AO}{\sqrt{SA^2+AO^2}}=\dfrac{a\sqrt{21}}{7}\)

\(\left\{{}\begin{matrix}AO\cap\left(SBC\right)=C\\AC=2OC\end{matrix}\right.\) \(\Rightarrow d\left(A;\left(SBC\right)\right)=2d\left(O;\left(SBC\right)\right)\)
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
Từ A kẻ \(AH\perp SB\Rightarrow AH\perp\left(SBC\right)\Rightarrow AH=d\left(A;\left(SBC\right)\right)\)
\(\dfrac{1}{AH^2}=\dfrac{1}{SA^2}+\dfrac{1}{AB^2}\Rightarrow AH=\dfrac{SA.AB}{\sqrt{SA^2+AB^2}}=\dfrac{a\sqrt{285}}{19}\)
\(\Rightarrow d\left(O;\left(SBC\right)\right)=\dfrac{1}{2}AH=\dfrac{a\sqrt{285}}{38}\)