Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Gọi R là bán kính đáy hộp sữa
\(\Rightarrow\)chiều cao hộp sữa là : \(3R\)
Thể tích hộp sữa là : \(\pi R^2\times3R=192\pi\Leftrightarrow R^3=64\Leftrightarrow R=4cm\)
Ơ mà sao lại hỏi thể tích nhỉ, đề cho luôn là \(192\pi cm^3\) mà nhỉ
Đáp án D
d = 8 c m ⇒ r = d 2 = 4 c m là bán kính đáy
Diện tích toàn phần của hộp sữa là: S t p = 2 π r h + π r 2 = 2 π .4.12 + π .4 2 = 112 π ( c m 2 ) (vì bỏ nắp nên chỉ có 1 đáy)
Bài làm :
Đường kính đáy và độ dài trục của hình trụ bằng nhau
=> Chiều cao h gấp 2 lần bán kính r
Ta có :
\(V=\pi.r^2.h\)
\(\Rightarrow16\pi=\pi.r^2.2r\)
\(\Rightarrow2.r^3=16\)
\(\Rightarrow r^3=8\)
\(\Rightarrow r=2\left(cm\right)\)
\(\Rightarrow h=2r=4\left(cm\right)\)
Vậy diện tích vật liệu cần dùng là ;
\(S_{tp}=2.\pi.r.h+2.\pi.r^2=16\pi+8\pi=24\pi\left(cm^2\right)\)
Gọi số đo đường kính đáy của hộp sữa là x (cm)→ Trục của hộp sữa là x→Bán kính đáy là \(\dfrac{1}{2}x\)
Vì thể tích hộp sữa là 16\(\pi\)⇒\(\left(\dfrac{1}{2}x\right)^2x=16\)⇔x=4→Bán kính đáy là 2cm
⇒Stp=2.\(\pi\).22.4+2.\(\pi\).22=40\(\pi\)
Bên trong hộp chứa được:
\(V=\text{π}.r^2h=\text{π}.\left(\dfrac{7}{2}\right)^2.8\approx3,14.\dfrac{7^2}{2^2}.8=307,72\left(cm^3\right)=307,72\left(ml\right)\)
Vậy bên trong hộp chứa được \(307,72\) ml
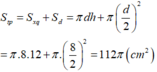
Gọi chiều cao là x
=>Bán kính là 0,4x
Theo đề, ta có; x*(0,4x)^2*pi=540*pi
=>0,16*x^3=540
=>x=15
=>Bán kính là 6cm
Diện tích vỏ hộp là:
2*pi*15*6+2*pi*15^2
=630pi(cm2)