Giúp mình với
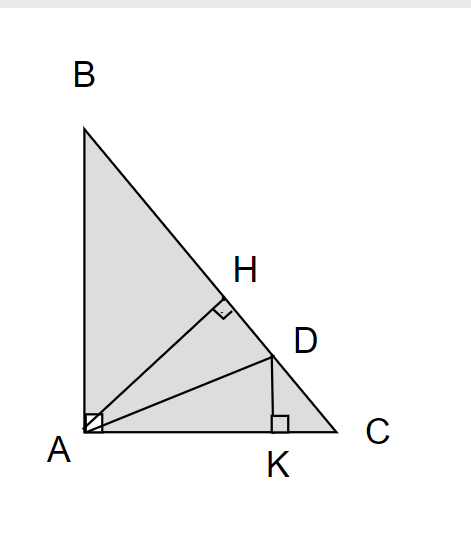
Cho tam giác ABC vuông tại A. Vẽ đường cao AH. Trên BC lấy D sao cho BD = BA
a. Cn góc BAD= góc ADB
b. Cm AD là đường phân giác của góc HAC
c. Vẽ DK vuông với AC. Cm AK = AH
d. Cm AB+ AC< BC+ 2AH
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 3 2018
a,: Vì tam giac BAD có BA=BD=>BAD cân tại A
=>góc BAD=góc ADB( 2 cạnh đáy tam giác cân)
b,:Vì góc BAD=góc BDA(Cm câu a),Mà BAD+DAC=900(A vuong)
=>BDA+DAC=900MÀ BDA+HAD=900(2 góc nhon trong tam giac vg thi fu nhau)
=>HAD=DAC
=>AD la dug phân giác góc HAC
Câu c,d tu lam nhe, mik mỏi tay
11 tháng 5 2022
a: Xét ΔBAD có BA=BD
nên ΔBAD cân tại B
hay \(\widehat{BAD}=\widehat{BDA}\)
b: Ta có: \(\widehat{CAD}+\widehat{BAD}=90^0\)
\(\widehat{HAD}+\widehat{BDA}=90^0\)
mà \(\widehat{BAD}=\widehat{BDA}\)
nên \(\widehat{CAD}=\widehat{HAD}\)
hay AD là tia phân giác của góc HAC
YP
11 tháng 5 2022
c, Ta có: Góc CAD= góc HAD
hay góc KAD= góc HAD
Xét △ AHD và △AKD có:
AD chung
Góc AHD= góc AKD= 90 độ
Góc KAD= góc HAD
=> △AHD= △AKD (cạnh huyền- góc nhọn)
=> AH= AK (2 cạnh tương ứng)
TN
22 tháng 4 2016
a) Xét tam giac BAD ta có : BA=BD (gt)=> tam giac BAD cân tại B => goc BAD= góc ADB
b) ta có
goc BAD + goc DAK =90 ( 2 góc kề phụ )
goc ADB + goc HAD =90 ( tamg iac AHD vuông tại H)
goc BAD = goc ADB ( cm câu a)
==> goc DAK = goc HAD
==> AD là phân giác góc HAC
c)Xét tam giac AHD vuông tại H và tam giac AKD vuông tại K ta có
AD=AD ( cạnh chung)
goc HAD = goc DAK ( AD la phân giác góc HAC)
--> tam giác AHD = tam giác AKD ( ch - gn )
--> AH= AK ( 2 cạnh tương ứng )
d) ta có ;
AB < BH + AH ( bất đẳng thức trong tam giac ABH )
AC < HC + AH ( bất đẳng thức trong tam giac AHC )
--> AB+AC < BH +AH + HC+ AH
--> AB + AC < BC + 2 AH
( chúc bạn thi tốt )
4 tháng 7 2021
a) Xét ΔBAD có BA=BD(gt)
nên ΔBAD cân tại B(Định nghĩa tam giác cân)
Suy ra: \(\widehat{BAD}=\widehat{BDA}\)(hai góc ở đáy)
b) Ta có: \(\widehat{CAD}+\widehat{BAD}=90^0\)(tia AD nằm giữa hai tia AB,AC)
\(\widehat{HAD}+\widehat{HDA}=90^0\)(ΔHAD vuông tại H)
mà \(\widehat{BAD}=\widehat{HDA}\)(cmt)
nên \(\widehat{CAD}=\widehat{HAD}\)
hay AD là tia phân giác của \(\widehat{HAD}\)
c) Xét ΔAHD vuông tại H và ΔAKD vuông tại K có
AD chung
\(\widehat{HAD}=\widehat{KAD}\)(AD là tia phân giác của \(\widehat{HAK}\))
Do đó: ΔAHD=ΔAKD(Cạnh huyền-góc nhọn)
Suy ra: AH=AK(hai cạnh tương ứng)
a, ta co AB = DB suy ra tam giac BAD can tai B (1)
từ (1) => góc BAD = góc ADB (DPCM)