gọi x1,x2 là nghiệm của phương trình : x2+x-2+√2=0 không giải phương trình tính các giá trị của biểu thức sau: D=X13+X32
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Phương trình x 2 − 20x − 17 = 0 có = 468 > 0 nên phương trình có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-ét ta có x 1 + x 2 = − b a x 1 . x 2 = c a ⇔ x 1 + x 2 = 20 x 1 . x 2 = − 17
Ta có
C = x 1 3 + x 2 3 = x 1 3 + 3 x 1 2 x 2 + 3 x 1 x 2 2 + x 2 3 − 3 x 1 2 x 2 − 3 x 1 x 2 2 = ( x 1 + x 2 ) 3 − 3 x 1 x 2 ( x 1 + x 2 ) = 2 3 – 3 . ( − 17 ) . 20 = 9020
Đáp án: D

Phương trình 2 x 2 − 18x + 15 = 0 có = 61 > 0 nên phương trình có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-ét ta có
Ta có
( x 1 + x 2 ) 3 = x 1 3 + 3 x 12 x 2 + 3 x 1 x 22 + x 2 3 ⇒ ( x 1 + x 2 ) 3 = x 1 3 + x 2 3 + 3 x 1 x 2 ( x 1 + x 2 ) ⇒ x 1 3 + x 2 3 = ( x 1 + x 2 ) 3 − 3 x 1 x 2 ( x 1 + x 2 )
Nên
C = x 1 3 + x 2 3 = x 1 + x 2 3 - 3 x 1 x 2 ( x 1 + x 2 )
= 9 3 – 3 . 3 . 15 2 = 1053 2
Đáp án: B

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-1\\x_1x_2=-2+\sqrt{2}\end{matrix}\right.\)
\(A=\dfrac{1}{x_1}+\dfrac{1}{x_2}=\dfrac{x_1+x_2}{x_1x_2}=\dfrac{-1}{-2+\sqrt{2}}=\dfrac{2+\sqrt{2}}{2}\)
\(B=x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=\left(-1\right)^2-2\left(-2+\sqrt{2}\right)=5-2\sqrt{2}\)

Đáp án B
Phương trình x 2 - 5 x + 2 = 0 có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-ét ta có:
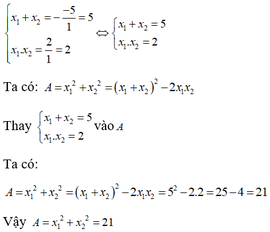

Phương trình x 2 − 5x + 2 = 0 có = ( − 5 ) 2 – 4.1.2 = 17 > 0 nên phương trình có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-ét ta có x 1 + x 2 = − b a x 1 . x 2 = c a ⇔ x 1 + x 2 = 5 x 1 . x 2 = 2
Ta có
A = x 1 2 + x 2 2 = ( x 1 + x 2 ) 2 – 2 x 1 . x 2 = 5 2 – 2 . 2 = 21
Đáp án: B

Đáp án B
Phương trình x 2 - 5 x + 2 = 0 có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-ét ta có:
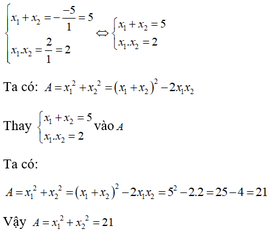

Phương trình: − x 2 − 4x + 6 = 0 có = ( − 4 ) 2 – 4.(− 1).6 = 40 > 0 nên phương trình có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-ét ta có x 1 + x 2 = − b a x 1 . x 2 = c a ⇔ x 1 + x 2 = − 4 x 1 . x 2 = − 6
Ta có
N = 1 x 1 + 2 + 1 x 2 + 2 = x 1 + x 2 + 4 x 1 x 2 + 2 x 1 + x 2 + 4 = − 4 + 4 − 6 + 2. − 4 + 4
Đáp án: C

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{5}{3}\\x_1x_2=-2\end{matrix}\right.\)
\(\dfrac{x_1}{x_2-1}+\dfrac{x_2}{x_1-1}=\dfrac{x_1\left(x_1-1\right)+x_2\left(x_2-1\right)}{\left(x_1-1\right)\left(x_2-1\right)}\)
\(=\dfrac{x_1^2+x_2^2-\left(x_1+x_2\right)}{x_1x_2-\left(x_1+x_2\right)+1}=\dfrac{\left(x_1+x_2\right)^2-2x_1x_2-\left(x_1+x_2\right)}{x_1x_2-\left(x_1+x_2\right)+1}\)
\(=\dfrac{\left(-\dfrac{5}{3}\right)^2-2.\left(-2\right)-\left(-\dfrac{5}{3}\right)}{-2-\left(-\dfrac{5}{3}\right)+1}=...\)

a) Ta có: \(2x^2-3x-2=0\)
nên a=2; b=-3 và c=-2
Vì \(x_1\) và \(x_2\) là nghiệm của phương trình \(2x^2-3x-2=0\) nên Áp dụng hệ thức Viet, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-b}{a}=\dfrac{3}{2}\\x_1\cdot x_2=-\dfrac{2}{2}=-1\end{matrix}\right.\)
Ta có: \(x_1\cdot x_2=-1\)
nên \(2\cdot x_1\cdot x_2=-2\)
Ta có: \(\left(x_1+x_2\right)^2=\left(\dfrac{3}{2}\right)^2=\dfrac{9}{4}\)
\(\Leftrightarrow x_1^2+x_2^2+2\cdot x_1\cdot x_2=\dfrac{9}{4}\)
\(\Leftrightarrow x_1^2+x_2^2=\dfrac{9}{4}+2=\dfrac{17}{4}\)
Lời giải:
Theo định lý Viet thì ta có:
$x_1+x_2=-1$
$x_1x_2=-2+\sqrt{2}$
Khi đó:
$D=(x_1+x_2)^3-3x_1x_2(x_1+x_2)=(-1)^3-3(-2+\sqrt{2})(-1)$
$=-1+3(-2+\sqrt{2})=-7+3\sqrt{2}$