Cho Δ ABC \(\sim\) Δ DEF theo tỉ số đồng dạng k = \(\dfrac{2}{3}\) , AH là đường cao của tam giác ABC ( H\(\in\) BC)
DI là đường cao của tam giác DEF ( I \(\in\) EF)
a. Tính tỉ số chu vi của tam giác ABC và tam giác DEF
b. Tính \(\dfrac{AH}{DI}\)
help me!!!

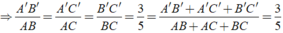
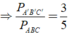
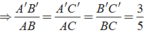
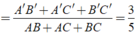
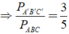
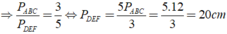

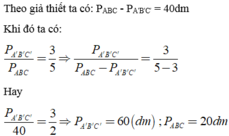
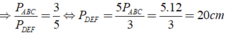
a: ΔABC đồng dạng vơi ΔDEF
=>\(\dfrac{C_{ABC}}{C_{DEF}}=k=\dfrac{2}{3}\)
b:AH/DI=k=2/3