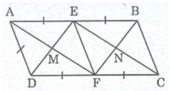
Cho hình bình hành ABCD, có AB=2AD. Gọi N, M lần lượt là trung điểm của AB, CD. Gọi H là giao điểm của AM và DN, gọi I là giao điểm của BM và CN.
a) Chứng minh ANMD và BCMN là hình thoi.
b) Chứng minh CN và ND vuông góc với nhau.
c) Chứng minh tam giác AHD và tam giác CND đồng dạng.
d) Nối A với C cắt DN tại E và cắt MB tại F. Chứng minh AE=EF=FC.
MỌI NGƯỜI GIÚP MIK VỚI Ạ. MAI MIK PHẢI NỘP RỒI :((
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 8:
a: Xét tứ giác AEFD có
AE//FD
AE=FD
Do đó: AEFD là hình bình hành
mà AE=AD
nên AEFD là hình thoi

a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành

Tứ giác AEFD là hình thoi
⇒ AF ⊥ ED ⇒ ∠ (EMF) = 90 0
AF // CE (vì tứ giác AECF là hình bình hành)
Suy ra: CE ⊥ ED ⇒ ∠ (MEN) = 90 0
Xét tứ giác EBFD, ta có: EB = FD (vì cùng bằng AE)
EB // FD (vì AB // CD)
Tứ giác EBFD là hình bình hành (vì có một cặp cạnh đổi song song và bằng nhau) ⇒ DE // BF
Suy ra: BF ⊥ AF ⇒ ∠ (MFN) = 90 0
Vậy tứ giác EMFN là hình chữ nhật.
a: Xét tứ giác ANMD có
AN//MD
AN=MD
AN=AD
=>ANMD là hình thoi
Xét tứ giác BCMN co
BN//CM
BN=CM
BN=BC
=>BCMN là hình thoi
b: Xét ΔNCD có
NM là trung tuyến
NM=CD/2
=>ΔNCD vuông tại N
c: Xét ΔAHD vuông tại H và ΔCND vuông tại N có
góc ADH=góc CDN
=>ΔAHD đồng dạng với ΔCND