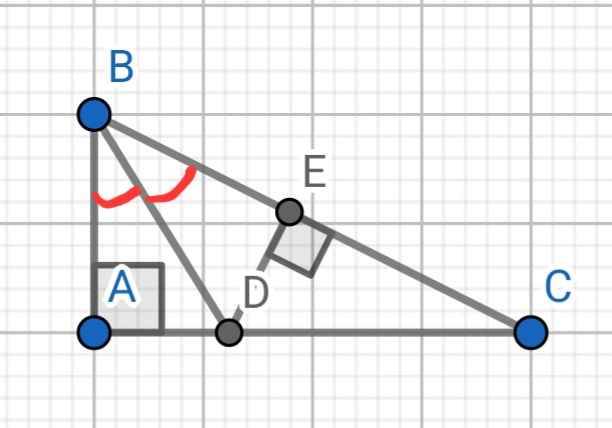
Tam giác ABC vuông tại A, có góc B= 60 độ. Tia phân giác của góc B cắt AC ở D. Từ D kẻ DE vuông góc với BC tại E
a) Chứng minh rằng BA=BE
b) Tính số đo góc EDC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KV
3 tháng 5 2023
a) Xét hai tam giác vuông: ∆ABD và ∆EBD có:
∠ABD = ∠EBD (BD là phân giác của B)
BD chung
⇒ ∆ABD = ∆EBD (cạnh huyền - góc nhọn)
⇒ BA = BE (hai cạnh tương ứng)
b) Do ∆ABC vuông tại A
⇒ ∠B + ∠C = 90⁰
⇒ ∠C = 90⁰ - ∠B
= 90⁰ - 60⁰
= 30⁰
∆DEC vuông tại E có
∠C = 30⁰
∠EDC + ∠C = 90⁰
⇒ ∠EDC = 90⁰ - ∠C
= 90⁰ - 30⁰
= 60⁰
.jpg)
3 tháng 1 2022
a: \(\widehat{C}=90^0-60^0=30^0\)
b: Xét ΔBAD và ΔBED có
BA=BE
\(\widehat{ABD}=\widehat{EBD}\)
BD chung
Do đó: ΔBAD=ΔBED
Suy ra: \(\widehat{BAD}=\widehat{BED}=90^0\)
hay DE⊥CB
30 tháng 4 2021
a) Xét ΔABD vuông tại B và ΔAED vuông tại E có
AD chung
\(\widehat{BAD}=\widehat{EAD}\)(AD là tia phân giác của \(\widehat{BAE}\))
Do đó: ΔABD=ΔAED(cạnh huyền-góc nhọn)
30 tháng 4 2021
b) Ta có: AD là tia phân giác của \(\widehat{BAC}\)(gt)
nên \(\widehat{DAC}=\dfrac{\widehat{BAC}}{2}=\dfrac{60^0}{2}=30^0\)(1)
Ta có: ΔABC vuông tại B(gt)
nên \(\widehat{C}+\widehat{A}=90^0\)(hai góc nhọn phụ nhau)
\(\Leftrightarrow\widehat{DCA}+60^0=90^0\)
hay \(\widehat{DCA}=30^0\)(2)
Từ (1) và (2) suy ra \(\widehat{DAC}=\widehat{DCA}\)
Xét ΔDCA có \(\widehat{DAC}=\widehat{DCA}\)(cmt)
nên ΔDCA cân tại D(Định lí đảo của tam giác cân)
Suy ra: DA=DC(hai cạnh bên)
Xét ΔAED vuông tại E và ΔCED vuông tại E có
DA=DC(cmt)
DE chung
Do đó: ΔAED=ΔCED(cạnh huyền-cạnh góc vuông)
Suy ra: EA=EC(hai cạnh tương ứng)
4 tháng 3 2020
Tự vẽ hình nha
a) ABD và EBD có: abd = ebd (bd la phân giác), BD chung
=> bằng nhau (cạnh huyền - góc nhọn)
=> AB = Be (2 cạnh tương ứng) => abe cân
b) ta có: AD = DE (vì tg ABD = tg EBD) mà DE < CD (Cạnh huyên là cạnh lớn nhất) nên AD < CD (ĐPCM)
14 tháng 3 2023
a: \(BC=\sqrt{9^2+12^2}=15\left(cm\right)\)
AD là phân giác
=>BD/CD=AB/AC=3/4
=>4DB=3CD
mà DB+DC=15
nên DB=45/7cm; DC=60/7cm
b: Xet ΔABC vuông tại A và ΔEDC vuông tại E có
góc C chung
=>ΔABC đồng dạng với ΔEDC
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
=>BA=BE
b: góc ADE=180-60=120 độ
=>góc EDC=60 độ