Cho tam giác nhọn ABC. Đường trung tuyến AM (M Î BC). Trên tia đối của tia MA lấy điểm D sao cho MA = MD a) Chứng minh DMAB = DMDC. b) Chứng minh CD // AB. c) Kẻ đường trung tuyến BN (N Î AC). Trên tia đối của tia NB lấy điểm E sao cho NB = NE. Chứng minh ba điểm E, C, D thẳng hàng.gấp ạ,giúp m voi.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

21 tháng 6 2021
giúp mik nhanh câu c dc khum ạ
2 câu kia mik xong r
cảm ơn các bạn

12 tháng 9 2015
a, áp dụng định lí pytago vào tam giác ABC ta có:
\(BC^2=AB^2+AC^2\)
\(BC^2=3^2+4^2=25\)
\(BC=\sqrt{25}=5\)
B, xét tam giác BAC và DCA có:
BM=MC
AM=MD
góc BMA= DMC (đối đỉnh)
=> Tam giác BAC=DCA
=>BA=DC
Góc BAM=MDC=>BA//DC(so le trong)
cho mk xin **** nah

10 tháng 5 2022
a: \(AC=\sqrt{15^2-9^2}=12\left(cm\right)\)
b: XétΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔMAB=ΔMDC

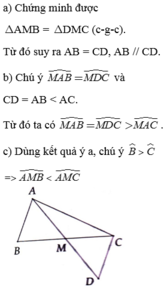
a: Xet ΔMAB và ΔMDC có
MA=MD
góc AMB=góc DMC
MB=MC
=>ΔMAB=ΔMDC
b: ΔMAB=ΔMDC
=>góc MAB=góc MDC
=>AB//CD
c: Xét tứ giác ABCE có
N là trung điểm chung của AC và BE
=>ABCE là hình bình hành
=>AB//EC
=>C,E,D thẳng hàng