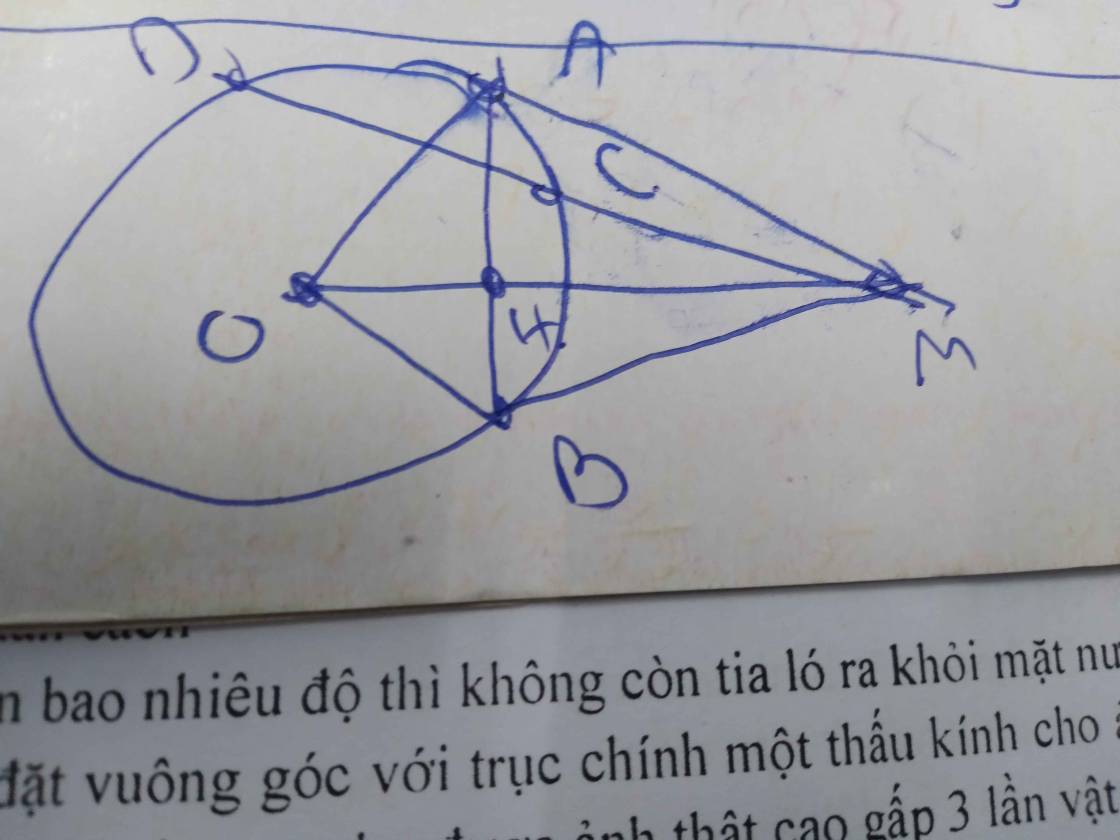
Cho điểm M nằm ngoài đường tròn tâm O.Kẻ hai tiếp tuyết MA và MB ( A, B là tiếp điểm ) và một cát tuyến MCD nằm giữa MO và MA ( MC<MD )với đường tròn. Lấy điểm I thuộc đoạn AB ( IB< IA ), I không thuộc cát tuyến MCD. Kẻ OH vuông MI tại H
a/ C/m : H , O , M , B , A cùng thuộc 1 đường tròn


vì AM là tiếp tuyến của ( O) => OA⊥AM =>ΔOAM vuông ở A
=> điểm A thuộc đường tròn đường kính OM
vì BM là tiếp tuyến của (O) => OB⊥BM =>ΔOBM vuông ở B
=> điểm B thuộc đường tròn đường kính OM
Vì OH⊥MI=>ΔOHM vuông tại H
=> điểm H thuộc đường tròn đường kính OM
=> 4 điểm O,A,M,B,H cùng thuộc đường tròn đường kính OM