cho tam giác ABC vuong tạiA có AB <AC, Trên tia đối của tia BC lấy điểm E sao cho BE=BA.Tia phân giác của góc B cắt Ac tại D.
(1) CM ràng : Tam giác BAD = Tam giác BED
2) Kẻ AK vuông góc vói BC (K ∊ BC).CM AK//De và AE là tia phân giác của góc DAK
3) Gọi H là giao điểm của BD và A. CM HB + HC <Ab + AC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
21 tháng 4 2023
Đúng(1)
Những câu hỏi liên quan
CT
6
HN
1
28 tháng 12 2020
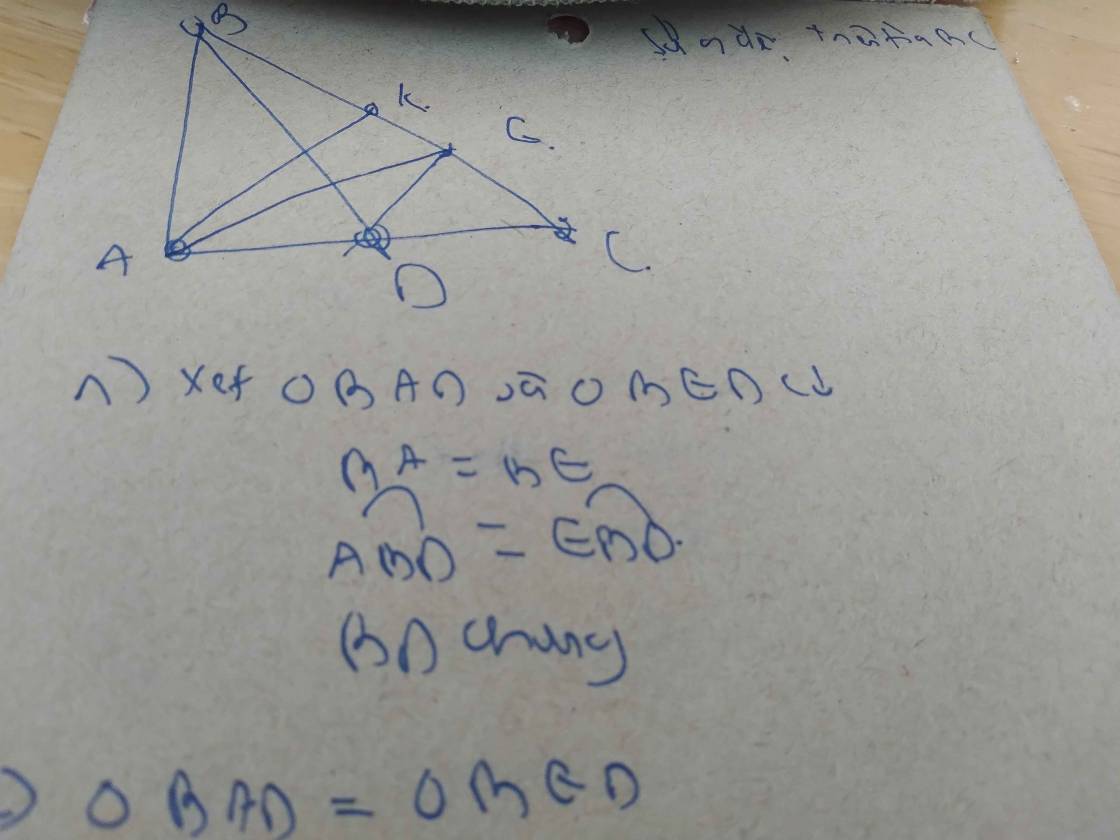
Áp dụng định lí Pytago vào ΔACH vuông tại H, ta được:
\(AC^2=CH^2+AH^2\)
\(\Leftrightarrow AH^2=AC^2-CH^2=20^2-16^2=144\)
hay AH=12(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow HB=\dfrac{AH^2}{HC}=\dfrac{12^2}{16}=9\left(cm\right)\)
Ta có: BC=BH+CH(H nằm giữa B và C)
nên BC=9+16=25(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AB^2=BC^2-AC^2=25^2-20^2=225\)
hay AB=15(cm)
Vậy: AB=15cm; AH=12cm; BC=25cm; BH=9cm
HN
1
28 tháng 12 2020
Áp dụng định lí Pytago vào ΔACH vuông tại H, ta được:
\(AC^2=BH^2+CH^2\)
\(\Leftrightarrow AC^2=5^2+12^2=169\)
hay AC=13(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow HB=\dfrac{AH^2}{HC}=\dfrac{12^2}{5}=28.8\left(cm\right)\)
Ta có: BC=HB+HC(H nằm giữa B và C)
nên BC=28,8+5=33,8(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow AB^2=BC^2-AC^2=33.8^2-13^2=973.44\)
hay \(AB=31.2cm\)
Vậy: AC=13cm; AB=31,2cm; BC=33,8cm; BH=28,8cm
28 tháng 12 2020
Áp dụng định lí Pytago vào ΔBAH vuông tại H, ta được:
\(AH^2+HB^2=AB^2\)
\(\Leftrightarrow HB^2=AB^2-AH^2=30^2-24^2=324\)
hay HB=18(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH^2=HB\cdot HC\)
\(\Leftrightarrow HC=\dfrac{AH^2}{HB}=\dfrac{24^2}{18}=32\left(cm\right)\)
Ta có: BC=HB+HC(H nằm giữa B và C)
nên BC=18+32=50(cm)
Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(AB^2+AC^2=BC^2\)
\(\LeftrightarrowÁC^2=BC^2-AB^2=50^2-30^2=1600\)
hay AC=40cm
Vậy: AC=40cm; CH=32cm; BC=50cm; BH=18cm
NT
0
7 tháng 5 2021
Xét tam giác amc = tam giác dmb có:
cạnh mc = mb[ giả thiết]
góc amc =dmb[2 góc đối đỉnh]
ta có bd song song với ac nên suy ra góc acm = góc mbd
=> tam giác amc = tam giác dmb [ g.c.g]
