Giúp em vs ạ
Câu hỏi: Cho ∆ABC vuông tại A có AB=15cm, AC=20cm. Vẽ AH vuông góc với BC tại H.
a) Chứng minh ∆HBA đồng dạng với ∆ABC
b) Tính độ dài các cạnh BC, HA
c) Vẽ tia phân giác của góc BAH cắt BH tại D. Tính độ dài các cạnh DB, DH
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NL
Nguyễn Lê Phước Thịnh
20 tháng 4 2023
Đúng(0)
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 4 2023
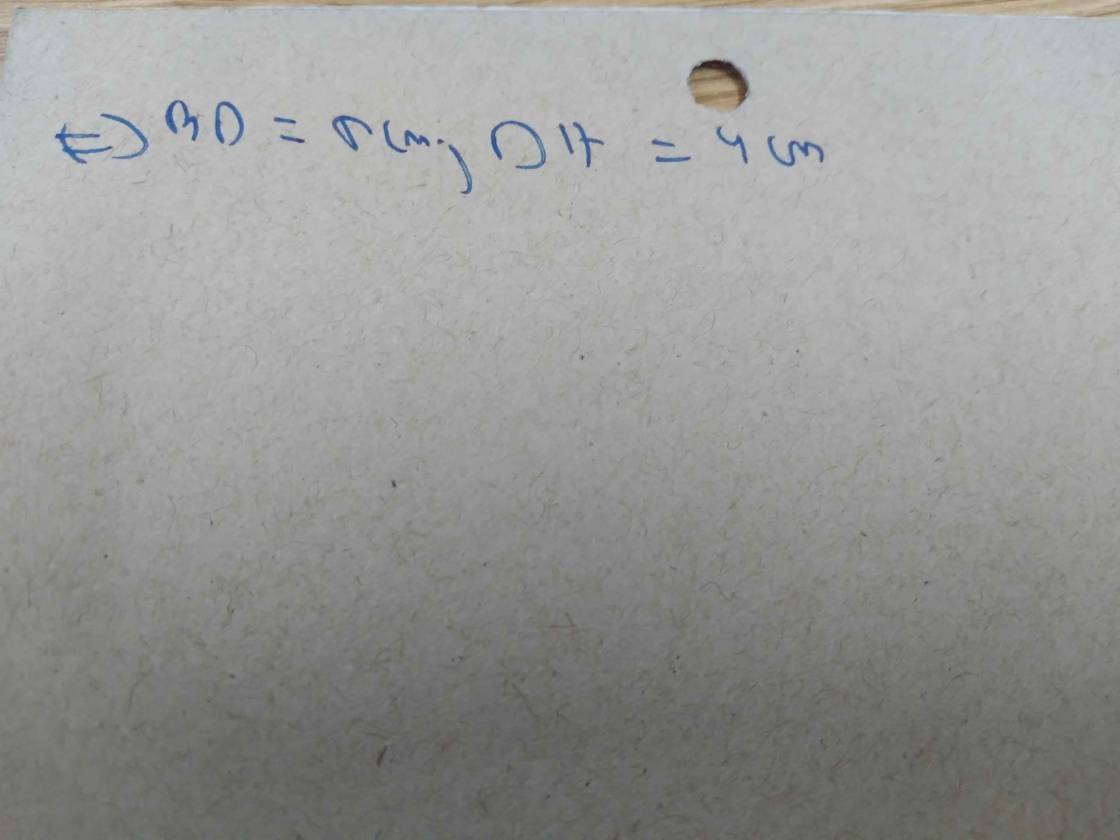
a.
Xét hai tam giác HBA và ABC có:
\(\left\{{}\begin{matrix}\widehat{B}\text{ chung}\\\widehat{BHA}=\widehat{BAC}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta HBA\sim\Delta ABC\left(g.g\right)\)
b.
Áp dụng định lý Pitago cho tam giác vuông ABC:
\(BC=\sqrt{AB^2+AC^2}=25\left(cm\right)\)
Từ câu a ta có: \(\dfrac{HA}{AC}=\dfrac{BA}{BC}\Rightarrow HA=\dfrac{AB.AC}{BC}=12\left(cm\right)\)
c.
Áp dụng định lý Pitago cho tam giác vuông HBA:
\(BH=\sqrt{AB^2-HA^2}=9\left(cm\right)\)
Do AD là phân giác, áp dụng định lý phân giác:
\(\dfrac{BD}{AB}=\dfrac{DH}{AH}\Rightarrow\dfrac{BD}{AB}=\dfrac{BH-BD}{AH}\)
\(\Rightarrow12BD=15\left(9-BD\right)\Rightarrow BD=5\left(cm\right)\)
\(\Rightarrow DH=BH-BD=4\left(cm\right)\)
14 tháng 3 2023
a. Xét tam giác HAC và tam giác ABC, có:
\(\widehat{C}\) : chung
\(\widehat{AHC}=\widehat{BAC}=90^o\)
Vậy tam giác \(HAC\sim\) tam giác \(ABC\) ( g.g )
b.\(\Rightarrow\dfrac{AH}{AB}=\dfrac{AC}{BC}\) (1)
Áp dụng định lý pytago tam giác ABC, ta có:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{15^2+20^2}=25\left(cm\right)\)
\(\left(1\right)\Leftrightarrow AH=\dfrac{AC.AB}{BC}=\dfrac{20.15}{25}=12\left(cm\right)\)
c. Tam giác AHB có phân giác AD:
\(\Rightarrow\dfrac{AH}{AB}=\dfrac{HD}{BD}\) (2)
(1)(2) \(\Rightarrow\dfrac{HD}{BD}=\dfrac{AC}{BC}\) hay \(\dfrac{BD}{HD}=\dfrac{BC}{AC}\)
TT
12 tháng 5 2021
Đọc câu cuối thì chắc là chứng minh phản chứng đêý ạ ( Ngu lí thuyết, chắc thế.)
Đại khái cái cách này là bạn gọi 1 trong 3,4 điểm cần cm thẳng hàng ý trùng 1 điểm bâts kì thuộc (hoặc chứng minh được) thuộc đoạn thẳng có 2 mút là 2 điểm cần chứng minh ấy. Rồi từ dữ kiện đề bài => 2 điểm trùng nhau => thẳng hàng. Cơ bản mình hiểu là vậyyy ..
13 tháng 4 2022
sao FC lại song song me do cùng vuông góc hc được .CF vuông góc với tia phân giác góc MEC mà chỉ
