Cho đường tròn (O) đường kính AB = 2R. Lấy điểm M nằm giữa hai điểm O và B, kẻ dây CD vuông góc với AB tại M. Gọi E là điểm trên cung nhỏ AC (E * A và E =C), N là giao điểm của BE và CD. 2) Chứng minh tam giác MNB đồng dạng với tam giác EAB và AC +BE.BN = 4R*. 3) Kẻ dây DK song song với dây BE. Chứng minh AK vuông góc với CE.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1: góc AMB=1/2*sđ cung AB=90 độ
góc EFB+góc EMB=90+90=180 độ
=>EFBM nội tiếp
2: góc AMC=1/2*sđ cung AC
góc AMD=1/2*sđcung AD
mà sđ cung AC=sđ cung AD
nên góc AMC=góc AMD
=>MA là phân giác của góc CMD
Xet ΔACE và ΔAMC có
góc ACE=góc AMC
góc CAE chung
=>ΔACE đồng dạng với ΔAMC
=>AC/AM=AE/AC
=>AC^2=AM*AE

a: góc AEB=góc AFB=90 độ
góc GHB+góc GEB=180 độ
=>GHBE nội tiếp
b: góc AFG+góc AHG=180 độ
=>AFGH nội tiếp
góc FEG=góc AKH
góc HEG=góc FBA
góc AKH=góc FBA
=>góc FEG=góc HEG
=>EG là phân giác của goc FEH
góc EFG=góc HKB
góc HFG=góc EAB
góc HKB=góc EAB
=>góc EFG=góc HFG
=>FG là phân giác của góc HFE
=>G là tâm đường tròn nội tiếp ΔFEH

Xét (O) có
\(\widehat{AEB}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{AEB}=90^0\)
Xét tứ giác BEFI có
\(\widehat{BEF}+\widehat{FIB}=180^0\)
nên BEFI là tứ giác nội tiếp
hay B,E,F,I cùng thuộc 1 đường tròn

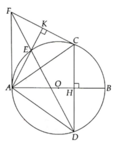
a, Học sinh tự chứng minh
b, DADB vuông tại D, có đường cao DH Þ A D 2 = AH.AB
c, E A C ^ = E D C ^ = 1 2 s đ E C ⏜ ; E A C ^ = K H C ^ (Tứ giác AKCH nội tiếp)
=> E D C ^ = K H C ^ => DF//HK (H là trung điểm DC nên K là trung điểm FC) => Đpcm
2: góc BEA=1/2*180=90 độ
Xét ΔBMN vuông tại M và ΔBEA vuông tại E có
góc MBN chung
=>ΔBMN đồng dạng với ΔBEA
=>BM/BE=BN/BA
=>BE*BN=BA*BM=BC^2
=>AC^2+BE*BN=AB^2=4*R^2