Giải Bất phương trình:(3x-1)(x2+1)<0
Giúp mik đi mn mik đag cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Điều kiện xác định x ≠ ±1.
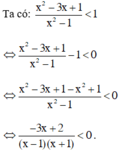
Đặt 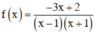 . Ta có bảng xét dấu:
. Ta có bảng xét dấu:
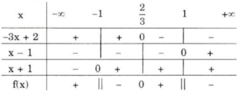
Dựa vào bảng xét dấu ta thấy 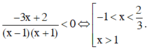
Vậy bất phương trình có tập nghiệm là 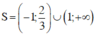

\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}2x-3\ge0\\2x-3\le-x^2+3x-1\end{matrix}\right.\\\left\{{}\begin{matrix}2x-3< 0\\3-2x\le-x^2+3x-1\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge\dfrac{3}{2}\\x^2-x-2\le0\end{matrix}\right.\\\left\{{}\begin{matrix}x< \dfrac{3}{2}\\x^2-5x+4\le0\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge\dfrac{3}{2}\\-1\le x\le2\end{matrix}\right.\\\left\{{}\begin{matrix}x< \dfrac{3}{2}\\1\le x\le4\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{3}{2}\le x\le2\\1\le x< \dfrac{3}{2}\end{matrix}\right.\) \(\Rightarrow1\le x\le2\)

Chọn C
ĐKXĐ:
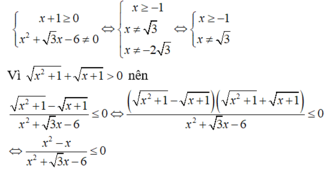
Bảng xét dấu
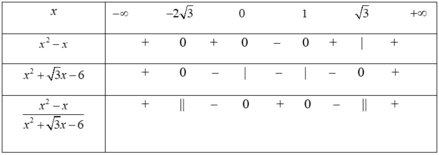
Dựa vào bảng xét dấu và đối chiếu điều kiện, ta có tập nghiệm của bất phương trình đã cho là
![]()

(2x – 1)(x + 3) – 3x + 1 ≤ (x – 1)(x + 3) + x2 – 5
⇔ 2x2 + 6x - x – 3 – 3x + 1 ≤ x2 + 3x - x – 3 + x2 – 5
⇔ 2x2 + 2x – 2 ≤ 2x2 + 2x – 8
⇔ 6 ≤ 0 (Vô lý).
Vậy BPT vô nghiệm.

a) Điều kiện: x + 2 ≠ 0 và x – 2 ≠ 0 ⇔ x ≠ ± 2
(Khi đó: x2 – 4 = (x + 2)(x – 2) ≠ 0)
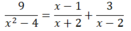
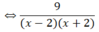
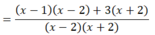
![]()
![]()
Vậy tập nghiệm của pt là: S = {-1; 1}
b) Điều kiện: 2x ≥ 0 ⇔ x ≥ 0
Khi đó: |x – 5| = 2x ⇔ x – 5 = 2x hoặc x – 5 = -2x
⇔ x = -5 hoặc x = 5/3
Vì x ≥ 0 nên ta lấy x = 5/3 . Tập nghiệm : S = {5/3}
c) x – 2)2 + 2(x – 1) ≤ x2 + 4
⇔ x2 – 4x + 4 + 2x – 2 ≤ x2 + 4
⇔ -2x ≤ 2
⇔ x ≥ -1
Tập nghiệm S = {x | x ≥ -1}

1.
\(6+2x\ge3-x\)
\(\Leftrightarrow3x\ge-3\)
\(\Leftrightarrow x\ge-1\)
2.
\(2x+7>16-x\)
\(\Leftrightarrow3x>23\)
\(\Leftrightarrow x>\dfrac{23}{3}\)
3.
\(x-5< 3x+1\)
\(\Leftrightarrow2x>-6\)
\(\Leftrightarrow x>-3\)
Mik chưa học đến lớp 8 nên ko bt biểu diễn trên trục số nên chỉ tìm dc x thôi nha:
1. 6 + 2x \(\ge\) 3 - x
<=> 6 - 3 \(\ge\) -x - 2x
<=> 3 \(\ge\) -3x
<=> 3 : (-3) \(\ge\) -3x : (-3)
<=> -1 \(\le\) x
<=> x \(\ge\) -1
2. 2x + 7 > 16 - x
<=> 2x + x > 16 - 7
<=> 3x > 9
<=> 3x : 3 > 9 : 3
<=> x > 3
3. x - 5 < 3x + 1
<=> -5 - 1 < 3x - x
<=> -6 < 2x
<=> -6 : 2 < 2x : 2
<=> -3 < x
<=> x > (-3)
Ta thấy : \(x^2+1\ge1\) nên để \(\left(3x-1\right)\left(x^2+1\right)< 0\)\(thì\) \(3x-1< 0\)\(hay\) \(x< \frac{1}{3}\)