Tìm hệ số của số hạng chứa x3 trong khai triển \(\left(x^3+\dfrac{1}{x}\right)^5\) (với x\(\ne\) 0)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HT
10 tháng 12 2020
Chắc là thế này \(3A^{n-2}_n\)
\(gt\Leftrightarrow2.n!-\left(4n+5\right)\left(n-2\right)!=3.\dfrac{n!}{2!}\)
\(\Leftrightarrow\dfrac{1}{2}n!=\left(4n+5\right)\left(n-2\right)!\Leftrightarrow\dfrac{1}{2}n\left(n-1\right)\left(n-2\right)!=\left(4n+5\right)\left(n-2\right)!\)
\(\Leftrightarrow\dfrac{1}{2}n\left(n-1\right)=4n+5\Leftrightarrow n=10\)
\(\left(3x^3-\dfrac{1}{x^2}\right)^{10}=\left(3x^3-x^{-2}\right)^{10}=\sum\limits^{10}_{k=0}C^k_{10}3^{10-k}.x^{3\left(10-k\right)}.\left(-1\right)^k.x^{-2k}\)
\(=\sum\limits^{10}_{k=0}C^k_{10}.\left(-1\right)^k.3^{10-k}.x^{30-5k}\)
=> so hang ko chua x: \(30-5k=0\Leftrightarrow k=6\)
\(\Rightarrow C^6_{10}.\left(-1\right)^6.3^{10-6}=17010\)
CM
27 tháng 6 2018
Đáp án là B
Ta có: x + 2 x 6 = ∑ k = 0 6 C 6 k 2 k x 6 − 3 2 k
Do đó số hạng chứa x 3 trong khai triển ứng với k thỏa mãn: 6 − 3 2 k = 3 ⇔ k = 2
Hệ số của x 3 trong khai triển là: C 6 2 2 2 = 60
20 tháng 12 2022
Câu 2:
\(\Leftrightarrow\dfrac{\left(n+2\right)!}{2!\cdot n!}-4\cdot\dfrac{\left(n+1\right)!}{n!\cdot1!}=2\left(n+1\right)\)
\(\Leftrightarrow\dfrac{\left(n+1\right)\left(n+2\right)}{2}-4\cdot\dfrac{n+1}{1}=2\left(n+1\right)\)
\(\Leftrightarrow\left(n+1\right)\left(n+2\right)-8\left(n+1\right)=4\left(n+1\right)\)
=>(n+1)(n+2-8-4)=0
=>n=-1(loại) hoặc n=10
=>\(A=\left(\dfrac{1}{x^4}+x^7\right)^{10}\)
SHTQ là: \(C^k_{10}\cdot\left(\dfrac{1}{x^4}\right)^{10-k}\cdot x^{7k}=C^k_{10}\cdot1\cdot x^{11k-40}\)
Số hạng chứa x^26 tương ứng với 11k-40=26
=>k=6
=>Số hạng cần tìm là: \(210x^{26}\)
JP
Tìm hệ số của số hạng chứa \(x^5\) trong khai triển đa thức \(f\left(x\right)=x\left(1-2x\right)^5\)
2
26 tháng 4 2023
Ta có: \(x.\left(C^k_n.a^{n-k}.b^k\right)=x.\left(C^k_5.a^{5-k}.b^k\right)=C^k_5.1^{5-k}.2^k.x^k.x\)
\(=C^k_5.2^k.x^{k+1}\)
Mà ta cần tìm số hạng của x5
\(\Rightarrow k+1=5\Leftrightarrow k=4\)
Vậy số hạng của x5 là: \(C^4_5.2^4=80\)
26 tháng 4 2023
Ta nhân thêm ''x'' vào số hạng tổng quát vì có ''x'' là nhân tử chung của mỗi số hạng trong khải triển
CM
5 tháng 11 2019
Đáp án A
Công thức khai triển nhị thức New-ton: a + b n = ∑ k = 0 n C n k a k b n − k .
Ta có:
x 3 − 3 x 12 = ∑ k = 0 12 C 12 k x 3 k − 3 x 12 − k = ∑ k = 0 12 C 12 k 1 3 k x k − 3 12 − k 1 x 12 − k
Số hạng chứa x 4 nên ta tìm k sao cho x k
x 12 − k = x 4 ⇔ x 2 k − 12 = x 4 ⇔ 2 k − 12 = 4 ⇔ k = 8.
Vậy hệ số của số hạng chứa x 4 là: C 12 8 . 1 3 8 . − 3 12 − 8 = C 12 8 3 4 = 55 9
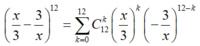
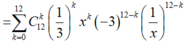
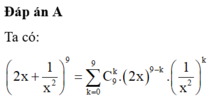
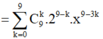
SHTQ là: \(C^k_5\cdot\left(x^3\right)^{5-k}\cdot\left(\dfrac{1}{x}\right)^k=C^k_5\cdot x^{15-4k}\)
Số hạng chứa x^3 tương ứng với 15-4k=3
=>4k=12
=>k=3
=>Hệ số là \(C^3_5=10\)