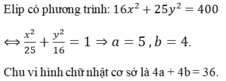Viết phương trình hình chữ nhật cơ sở của Elip x2/1 + y2/2/3 = 1 Giúp mình với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
EO
0
CM
31 tháng 1 2017
Đáp án: C
4 x 2 + 9 y 2 = 36
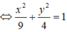
Elip có a 2 = 9 ⇒ a = 3, b 2 = 4 ⇒ b = 2
Hình chữ nhật cơ sở có hai cạnh là 2a = 6, 2b = 4. Do đó, diện tích hình chữ nhật cơ sở là: 6.4 = 24
PT
1
CM
8 tháng 12 2018
Đáp án: C
(E): 4
x
2
+ 5
y
2
= 20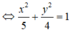 
Ta có: a 2 = 5 ⇒ a = 5 , b 2 = 4 ⇒ b = 2
Hình chữ nhật cơ sở có độ dài hai cạnh lần lượt là 2a = 2 5 , 2b = 4
Suy ra, diện tích hình chữ nhật cơ sở là: 2 5 .4 = 8 5
CM
20 tháng 2 2018
Gọi phương trình chính tắc của Elip có dạng
Các đỉnh của hình chữ nhật cơ sở có tọa độ: (a; b) ; (a; -b) ; ( -a; b) và (-a; -b)
Ta có M( 4;3) là một đỉnh của hình chữ nhật cơ sở nên chọn
.
=> phương trình chính tắc của (E) là
Chọn A.
CM
21 tháng 7 2017
Ta có độ dài trục nhỏ bằng 8 nên 2b = 8 b = 4
Hình chữ nhật cơ sở có chu vi bằng 40 nên 4a + 4b = 40
Mà b = 4 nên a= 6
Phương trình chính tắc của (E): x 2 36 + y 2 16 = 1
Đáp án A
CM
5 tháng 12 2018
Ta có
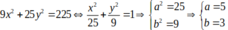
Độ dài trục lớn ( chiều dài hình chữ nhật cơ sở ): 2a= 10 .
Độ dài trục nhỏ ( chiều rộng hình chữ nhật cơ sở : 2b= 6
Diện tích hình chữ nhật cơ sở là 2a. 2b= 10.6= 60 .
Chọn C.
