Bài 20 (trang 110 SGK Toán 9 Tập 1)
Cho đường tròn tâm $O$ bán kính 6cm và một điểm $A$ cách $O$ là 10cm. Kẻ tiếp tuyến $AB$ với đường tròn ($B$ là tiếp điểm). Tính độ dài $AB$.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KD
25 tháng 4 2017
Dùng định lý Py-ta-go tính:
Tam giác OAB vuông tại B nên:
AB2 = OA2 – OB2 = 102 -62 =64
⇒ AB = 8
được AB=8cm.
30 tháng 9 2021
Bài 2:
Xét ΔOAB vuông tại B có
\(OA^2=OB^2+AB^2\)
hay AB=8(cm)
13 tháng 10 2021
a: Xét ΔOAB vuông tại B có
\(OA^2=OB^2+AB^2\)
hay AB=8(cm)
10 tháng 10 2021
Vì AB là tiếp tuyến (O;OB)
=> OB vuông AB
hay tam giác ABO vuông tại B
Xét tam giác OBA vuông tại B, đường cao BH
* Áp dụng hệ thức : \(OB^2=OH.OA\Rightarrow OH=\dfrac{OB^2}{OA}=\dfrac{18}{5}\)cm
\(=\sqrt{64}=8\left(cm\right)\)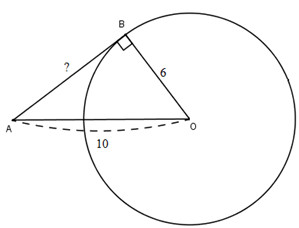
Áp dụng định lý Pytago vào tam giác AOB vuông tại B, ta có:
AB=\(\sqrt{AO^2-OB^2}=\sqrt{10^2-6^2}\)\(=\sqrt{64}=8\left(cm\right)\)
AB=8