Cho hai đường tròn (O; R) và (O'; R') cắt nhau tại A và H (O và O' ở hai phía của A). Vẽ các đường kính AOB và AO'C của hai đường tròn. Một đường thẳng d qua A cắt đường tròn (O) tại M, cắt đường tròn (O') tại N. A nằm giữa M và N Gọi I, K lần lượt là trung điểm M, N và BC
a. Chứng minh rằng bốn điểm A, H, I, K thuộc một đường tròn.
b. Xác định vị trí của đường thẳng d để diện tích tam giác HMN lớn nhất.


 ΔPBO
ΔPBO

 ΔPBO
ΔPBO
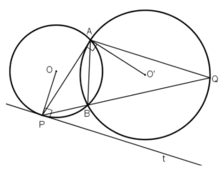


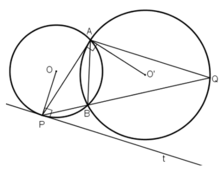


a: góc BMA=góc CNA=90 độ
=>MB//NC
=>IK//MB//NC
=>IK vuông góc MN
góc AIK+góc AHK=90+90=180 độ
=>AHIK nội tiếp
b: ΔHMN đồng dạng với ΔABC
=>góc MHN=góc BAC cố định
\(S_{HMN}=\dfrac{1}{2}\cdot HM\cdot HN\cdot sin\widehat{MHN}< =\dfrac{1}{2}\cdot AB\cdot AC\cdot sin\widehat{BAC}\)
Dấu = xảy ra khi MH là đừog kính của (O) và NH là đường kính của (O')