Cho đa thức
F(x)=x5 - 3x2 -x3 - x2 - 2x + 5
G(x)+x5 - x4 + x2 - 3x + x2 + 1
Tính H(x) = F(x) + G(x)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NN
2
Những câu hỏi liên quan
15 tháng 8 2021
a: \(F\left(x\right)=x^5-3x^2+x^3-x^2-2x+5\)
\(=x^5+x^3-4x^2-2x+5\)
\(G\left(x\right)=x^5-x^4+x^2-3x+x^2+1\)
\(=x^5-x^4+2x^2-3x+1\)
b: Ta có: \(H\left(x\right)=F\left(x\right)+G\left(x\right)\)
\(=x^5+x^3-4x^2-2x+5+x^5-x^4+2x^2-3x+1\)
\(=2x^5-x^4+x^3-2x^2-5x+6\)
HA
1
3 tháng 5 2022
\(f\left(x\right)-g\left(x\right)=\left(x^5-3x^2+x^3-x^2-2x+5\right)-\left(x^2-3x+1+x^2-x^4+x^5\right)\)
\(f\left(x\right)-g\left(x\right)=x^5-3x^2+x^3-x^2-2x+5-x^2+3x-1-x^2+x^4-x^5\)
\(f\left(x\right)-g\left(x\right)=\left(x^5-x^5\right)+\left(-3x^2-x^2-x^2-x^2\right)+x^3+\left(-2x+3x\right)+\left(5-1\right)+x^4\)
\(f\left(x\right)-g\left(x\right)=-6x^2+x^3+x+4+x^4\)
\(f\left(x\right)-g\left(x\right)=x^4+x^3-6x^2+x+4\)
CM
24 tháng 8 2017
Thu gọn, sắp xếp đa thức theo lũy thừa giảm của biến:
* Ta có: f(x) = x5 – 3x2 + x3 – x2 – 2x + 5
= x5 – (3x2 + x2 ) + x3 - 2x + 5
= x5 – 4x2 + x3 – 2x + 5
= x5 + x3 – 4x2 – 2x + 5
Và g(x) = x2 – 3x + 1 + x2 – x4 + x5
= (x2 + x2 ) – 3x + 1 – x4 + x5
= 2x2 – 3x + 1 – x4 + x5
= x5 – x4 + 2x2 – 3x + 1
* f(x) + g(x):
1 tháng 4 2018
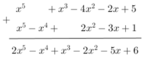
Thu gọn, sắp xếp đa thức theo lũy thừa giảm của biến:
* Ta có: f(x) = x5 – 3x2 + x3 – x2 – 2x + 5 = x5 + x3 – 4x2 – 2x + 5
g(x) = x2 – 3x + 1 + x2 – x4 + x5 = x5 – x4 + 2x2 – 3x + 1
* f(x) + g(x):
1 tháng 4 2018
Thu gọn, sắp xếp đa thức theo lũy thừa giảm của biến:
* Ta có: f(x) = x5 – 3x2 + x3 – x2 – 2x + 5 = x5 + x3 – 4x2 – 2x + 5
g(x) = x2 – 3x + 1 + x2 – x4 + x5 = x5 – x4 + 2x2 – 3x + 1
* f(x) + g(x): tự làm nha bạn
CM
15 tháng 2 2018
Ta có: f(x) + g(x) – h(x)
= (x5 – 4x3 + x2 – 2x + 1) + (x5 – 2x4 + x2 – 5x + 3) – (x4 – 3x2 + 2x – 5)
= x5 – 4x3 + x2 – 2x + 1 + x5 – 2x4 + x2 – 5x + 3 – x4 + 3x2 - 2x + 5
= (x5 +x5) – (2x4 + x4) – 4x3 + (x2 + x2 + 3x2)- (2x + 5x + 2x) + (1 + 3 + 5)
= (1 + 1)x5 – (2 + 1)x4 – 4x3 + (1 + 1 + 3)x2 - (2 + 5 + 2)x + (1 + 3 + 5)
= 2x5 – 3x4 – 4x3 + 5x2 – 9x + 9
6 tháng 8 2019
\(Tacó:f\left(x\right)+g\left(x\right)=x^5-x^3+x^2-2x+5+x^2-3x+1+x^2-x^4+x^5\)
6 tháng 8 2019
Ta có : j(x) + g(x) = (x5 - x3 - x2 - 2x +5 )+( x2 - 3x + 1 + x2 - x4 + x5)
= x5 - x3 - x2 - 2x +5+x2 - 3x + 1 + x2 - x4 + x5
=(x5 + x5) + (-3x - 3x) + (-2x+2x-2x)+ (5 +1) -4x
= 10x - 6x - 2x +6 - 4x
= -2x +6
Vậy j(x) + g(x) = -2x +6
CM
1 tháng 1 2017
f(x) = x5 + 3x2 − 5x3 − x7 + x3 + 2x2 + x5 − 4x2 + x7
= (x5 + x5) + (3x2 + 2x2 – 4x2) + (-5x3 + x3) + (-x7 + x7)
= 2x5 + x2 – 4x3.
= 2x5 - 4x3 + x2
Đa thức có bậc là 5
g(x) = x4 + 4x3 – 5x8 – x7 + x3 + x2 – 2x7 + x4 – 4x2 – x8
= (x4 + x4) + (4x3 + x3) – (5x8 + x8) – (x7 + 2x7) + (x2 – 4x2)
= 2x4 + 5x3 – 6x8 – 3x7 – 3x2
= -6x8 - 3x7 + 2x4 + 5x3 - 3x2.
Đa thức có bậc là 8.
CM
3 tháng 7 2018
* Ta có:
f(x) = x5 – 3x2 + 7x4 – 9x3 + x2 - 1/4 x
= x5 – (3x2 – x2) + 7x4 – 9x3 -1/4.x
= x5 – 2x2 + 7x4 – 9x3 -1/4.x
= x5 + 7x4 – 9x3 – 2x2 - 1/4
g(x) = 5x4 – x5 + x2 – 2x3 + 3x2 - 1/4
= 5x4 –x5+ (x2 + 3x2) – 2x3 – 1/4
= 5x4 – x5 + 4x2 – 2x3 – 1/4
= -x5 + 5x4 – 2x3 + 4x2 - 1/4
* f(x) + g(x)
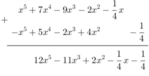
* f(x) - g(x)
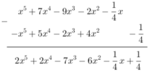
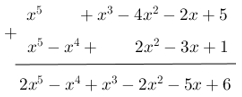
\(H\left(x\right)=F\left(x\right)+G\left(x\right)=\left(x^5-3x^2-x^3-x^2-2x+5\right)+\left(x^5-x^4+x^2-3x+x^2+1\right)\\ =x^5-3x^2-x^3-x^2-2x+5+x^5-x^4+x^2-3x+x^2+1\\ =\left(x^5+x^5\right)-x^4-x^3-\left(3x^2+x^2-x^2-x^2\right)-\left(2x+3x\right)+5\\ =2x^5-x^4-x^3-2x^2-5x+5\)
A =&@&@&#&#&÷&-^#<÷&
Cu