Tính ttoongr giúp mik câu C,D vs ạ
K
Khách
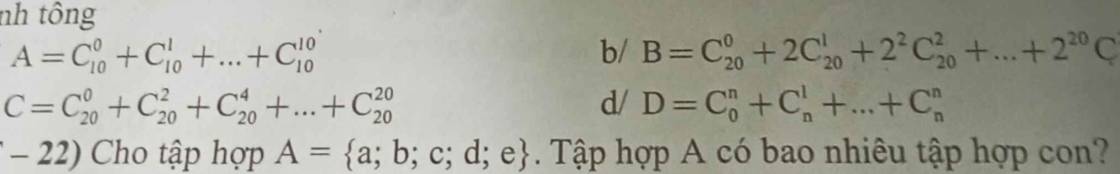
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 9 2021
\(D=10\cdot\left(-2.5\right)\cdot0.4\cdot\left(-0.1\right)\)
\(=10\cdot1\cdot2.5\cdot0.4\)
=10
7 tháng 2 2022
c) \(\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{12}\le x\le\dfrac{7}{10}+\dfrac{27}{6}\)
\(\Leftrightarrow\dfrac{2}{3}\le x\le\dfrac{26}{5}=5,2\), mà \(x\in Z\)
\(\Rightarrow x\in\left\{1;2;3;4;5\right\}\)
d) \(-\dfrac{31}{14}+\dfrac{115}{131}+\dfrac{111}{74}\le x\le\dfrac{6}{36}+\dfrac{9}{27}+\dfrac{48}{96}\)
\(\Leftrightarrow\dfrac{150}{917}\le x\le1\) , mà \(x\in Z\)
\(\Rightarrow x=1\)
TK
1
17 tháng 10 2021
Câu 3:
a: Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{3}=\dfrac{y}{2}=\dfrac{x+y}{3+2}=\dfrac{90}{5}=18\)
Do đó: x=54; y=36
TN
1
14 tháng 5 2022
Câu 3:
3)
d) \(3x^2+x-6-\sqrt{2}=0\)
\(\Leftrightarrow x^2+\dfrac{1}{3}x-2-\dfrac{\sqrt{2}}{3}=0\)
\(\Leftrightarrow x^2+\dfrac{1}{3}x-\dfrac{6+\sqrt{2}}{3}=0\)
\(\Leftrightarrow x^2+2.\dfrac{1}{6}x+\dfrac{1}{36}-\dfrac{6+\sqrt{2}}{3}-\dfrac{1}{36}=0\)
\(\Leftrightarrow\left(x+\dfrac{1}{6}\right)^2-\dfrac{73+12\sqrt{2}}{36}=0\)
\(\Leftrightarrow\left(x+\dfrac{1}{6}+\dfrac{\sqrt{73+12\sqrt{2}}}{6}\right)\left(x+\dfrac{1}{6}-\dfrac{\sqrt{73+12\sqrt{2}}}{6}\right)=0\)
\(\Leftrightarrow x=\dfrac{-1\pm\sqrt{73+12\sqrt{2}}}{6}\)
-Vậy \(S=\left\{\dfrac{-1\pm\sqrt{73+12\sqrt{2}}}{6}\right\}\)
12 tháng 2 2023
d: Xét tứ giác NKCM có
NK//CM
NK=CM
=>NKCM là hình bình hành
=>NC cắt KM tại trung điểm của mỗi đường
=>M,I,K thẳng hàng
9 tháng 12 2021
\(R_{tđ}=R_1+R_2=100+80=180\Omega\)
\(I_1=I_2=I=\dfrac{U}{R}=\dfrac{210}{180}=\dfrac{7}{6}A\)
Chiều dài 1 vòng quấn:
\(C=\pi\cdot d=0,25\pi\left(m\right)\)
Chiều dài dây dẫn:
\(l=n\cdot C=120\cdot0,25\pi=94,25m\)
Tiết diện dây:
\(S=\rho\dfrac{l}{R_2}=0,5\cdot10^{-6}\cdot\dfrac{94,25}{80}=5,89\cdot10^{-7}m^2\)
9 tháng 12 2021
a) vì R1 mắc nối tiếp với R2
=> Rtđ=R1+R2=100+80=180 (Ω)
b) cường độ dòng điện qua mỗi điện trở và mạch chính là :
I=I1=I2=U/Rtđ=240/180=4/3 (A)
c) chiều dài 1 vòng quấn là :
l1=3,14.0,025=0,0785m
chiều dài dây dẫn là
l=120.0,0785=9,42 vòng
tiết diện của dây dẫn là
R=p. l/S => S= l.p/R =0,5.10^-6 .9,42/80=5,89.10^-8 m^2
mn giúp mik câu c vs ạ
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 12 2021
\(B=\dfrac{\sqrt{x}}{\sqrt{x}-2}\Rightarrow C=\dfrac{x+3}{\sqrt{x}}=\sqrt{x}+\dfrac{3}{\sqrt{x}}\ge2\sqrt{\dfrac{3\sqrt{x}}{\sqrt{x}}}=2\sqrt{3}\)
Dấu "=" xảy ra khi \(\sqrt{x}=\dfrac{3}{\sqrt{x}}\Rightarrow x=3\)
c/Theo công thức pascal trong Nhị Thức Newton ta có: \(C_{n-1}^{n-1}\) + \(C_{n-1}^k\) = \(C_n^k\)
C = \(C_{19}^0\) + \(C_{19}^1\) + \(C_{19}^2\) + ....+ \(C_{19}^{18}\) + \(C_{19}^{19}\)
C = (1+1)19 = 524288
còn câu d hình như đề sai