1 hộp đựng 9 quả cầu xanh, 7 quả cầu đỏ , 8 quả cầu vàng. Chọn ra 5 quả cầu. Tính xác suất lấy được 5 quả cầu trong đó có ít nhất 1 quả cầu đỏ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 1 2021
a, có 2 quả đỏ, 1quả xanh, và 1 vàng : 9C2 x 5C2 x 4C2 =2160cách
b, ta có nếu chọn 6 quả ko cần thứ tự trừ đi cho ko có quả đỏ nào: 18C6 - 14C6=15561 cách
mình viết theo cách bấm trên máy tính mong bạn thông cảm.
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 1 2021
Số cách chọn có đúng 2 quả đỏ:
\(C_4^2.C_{14}^4=6006\) cách
Câu b thì bạn kia làm đúng rồi
CM
18 tháng 9 2019
Đáp án B
Lấy ngẫu nhiên từ mỗi hộp ra 1 quả cầu có
C 12 1 . C 10 1 = 120 cách
Lấy ngẫu nhiên từ mỗi hộp ra 1 quả cầu có
C 7 1 . C 6 1 = 42 cách
Vậy xác suất cần tính là P = 42 120 = 7 20
CM
6 tháng 3 2019
Đáp án B
Lấy ngẫu nhiên từ mỗi hộp ra 1 quả cầu có C 12 1 . C 10 1 = 120 cách.
Số cách để 2 quả cầu lấy ra cùng màu đỏ là C 7 1 . C 6 1 = 42 cách.
Vậy xác suất cần tính là P = 42 120 = 7 20 .
CM
16 tháng 3 2019
Đáp án B
Lấy mỗi hộp 1 quả cầu có: C 12 1 . C 10 1 = 120 quả cầu.
Gọi A là biến cố: 2 quả cầu lấy ra cùng màu đỏ.
Khi đó: Ω A = C 7 1 . C 6 1 = 42 .
Do đó xác suất cần tìm là: P ( A ) = 42 120 = 7 20 .
CM
4 tháng 9 2019
Đáp án B
Lấy mỗi hộp 1 quả cầu có: C 12 1 . C 10 1 = 120 quả cầu
Gọi A là biến cố: 2 quả cầu lấy ra cùng màu đỏ.
Khi đó: Ω A = C 7 1 . C 6 1 = 42
Do đó xác suất cần tìm là: P A = 42 120 = 7 20
CM
16 tháng 7 2017
Chọn D
Gọi Ω là không gian mẫu, ta có n( Ω ) = C 15 6 = 5005.
Gọi A là biến cố: “6 quả lấy được có đủ ba màu”
A ¯ : “6 quả lấy được không có đủ ba màu”.
TH1: 6 quả lấy được chỉ một màu đỏ có C 6 6 = 1cách.
TH2: 6 quả lấy được có hai màu
+ 6 quả lấy được có hai màu đỏ và xanh: có 
cách.
+ 6 quả lấy được có hai màu đỏ và vàng: có 
cách.
+ 6 quả lấy được có hai màu đỏ và xanh: có 
cách.
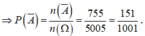
Vậy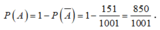 
CM
20 tháng 7 2017
Chọn A
Gọi T là phép thử lấy mỗi hộp ra một quả. Số phần tử của không gian mẫu trong phép thử T là
Gọi A là biến cố hai quả lấy ra từ mỗi hộp đều là màu đỏ. Số phần tử của biến cố A là: 
.
Vậy xác suất của biến cốA là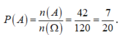 
.
VT
Vũ Thị Minh Ánh
Giáo viên
19 tháng 12 2022
1) \(\left(1+x\right)^6=\sum\limits^6_{k=0}C^k_6x^k\)
Số hạng chứa \(x^4\) có \(k=4\)
Hệ số của \(x^4\) trong khai triển là: \(C_6^4=15\).
2)
\(n\left(\Omega\right)=C_{20}^2=190\)
A: "Hai quả được chọn khác màu"
\(\overline{A}\): "Hai quả được chọn cùng màu".
\(n\left(\overline{A}\right)=C_{15}^2+C_5^2=115\)
\(n\left(A\right)=190-115=75\)
\(P\left(A\right)=\dfrac{75}{190}=\dfrac{15}{38}\)
Có: `\Omega =C_24 ^5`
Gọi `A:` "Lấy được `5` quả cầu trong đó có ít nhất `1` quả cầu đỏ."
`=>\overline{A}=C_17 ^5`
`=>P(A)=1-[C_17 ^5]/[C_24 ^5]=1297/1518`