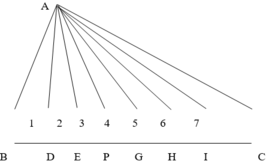
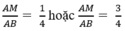Cho hình chữ nhật ABCD . Trên cạnh AB lấy 5 điểm và trên cạnh CD lấy 6 điểm . Nối đỉnh C và đỉnh D với mỗi điểm thuộc cạnh AB. Nối đỉnh A và đỉnh B với mỗi điểm thuộc cạnh CD . Hỏi có bao nhiêu tam giác có các đỉnh nằm trên các cạnh của hình chữ nhật được tạo thành
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 7 2017
Ta nhận xét :
- khi lấy 1 điểm thì tạo thành 2 tam giác đơn ABD và ADC. Số tam giác đếm được là 3 : ABC, ADB và ADC. Ta có : 1 + 2 = 3 (tam giác)
- khi lấy 2 điểm thì tạo thành 3 tam giác đơn và số tam giác đếm được là 6 :
ABC, ABD, ADE, ABE, ADC và AEC. Ta có : 1+ 2 + 3 = 6 (tam giác)
Vậy khi lấy 6 điểm ta sẽ có 7 tam giác đơn được tạo thành và số tam giác đếm được là : 1 + 2 + 3 + 4 + 5 + 6 + 7 = 28 (tam giác)
Cách 2 :- Nối A với mỗi điểm D, E, …, C ta được một tam giác có cạnh AD. Có 6 điểm như vậy nên có 6 tam giác chung cạnh AD (không kể tam giác ADB vì đã tính rồi)
Lập luận tương tự như trên theo thứ tự ta có 5, 4, 3, 2, 1 tam giác chung cạnh AE, AP, …, AI.
Vậy số tam giác tạo thành là : 7 + 6 + 5 + 4 +3 +2 + 1 = 28 (tam giác).
26 tháng 12 2016
Có 16 hình tam giác được tạo thành
Ai k mình mình k lại nhưng phải gửi tin nhắn cho mình hoặc kết bạn với mình
Thanks
CM
15 tháng 8 2017
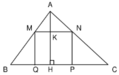
Vì ∆ ABC đồng dạng với ∆ AMN nên:
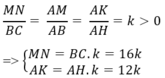
Diện tích hình chữ nhật MNPQ là:
SMNPQ = MN. NP = MN.KH = MN.( AH – AK)
=> SMNPQ = 16k.( 12- 12k)
Theo đề bài diện tích hình chữ nhật đó là 36cm2 nên
16k.( 12- 12k ) = 36
⇔ 16k.12( 1- k) = 36
⇔ 16k(1 – k) = 3 ( chia cả hai vế cho 12)
⇔ 16k – 16k2 = 3
⇔ 16k2- 16k + 3= 0
Ta có: ∆’= (-8)2 – 16.3 = 16> 0
Phương trình trên có 2 nghiệm là:
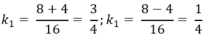
Vậy để diện tích hình chữ nhật MNPQ là 36cm2 thì vị trí điểm M phải thỏa mãn:
CM
22 tháng 10 2019
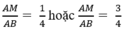
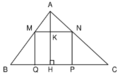
Vì ∆ ABC đồng dạng với ∆ AMN nên:
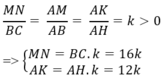
Diện tích hình chữ nhật MNPQ là:
SMNPQ = MN. NP = MN.KH = MN.( AH – AK)
=> SMNPQ = 16k.( 12- 12k)
Theo đề bài diện tích hình chữ nhật đó là 36cm2 nên
16k.( 12- 12k ) = 36
⇔ 16k.12( 1- k) = 36
⇔ 16k(1 – k) = 3 ( chia cả hai vế cho 12)
⇔ 16k – 16k2 = 3
⇔ 16k2- 16k + 3= 0
Ta có: ∆’= (-8)2 – 16.3 = 16> 0
Phương trình trên có 2 nghiệm là:
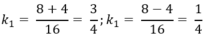
Vậy để diện tích hình chữ nhật MNPQ là 36cm2 thì vị trí điểm M phải thỏa mãn:
