Giải phương trình:6x4 + 8x2 + 6 = (x4 + 2x2 + 1) (1 + 4y -...
Đọc tiếp
Giải phương trình:
6x4 + 8x2 + 6 = (x4 + 2x2 + 1) (1 + 4y - y2)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 6 2023
2:
\(A=\dfrac{x_2-1+x_1-1}{x_1x_2-\left(x_1+x_2\right)+1}\)
\(=\dfrac{3-2}{-7-3+1}=\dfrac{1}{-9}=\dfrac{-1}{9}\)
B=(x1+x2)^2-2x1x2
=3^2-2*(-7)
=9+14=23
C=căn (x1+x2)^2-4x1x2
=căn 3^2-4*(-7)=căn 9+28=căn 27
D=(x1^2+x2^2)^2-2(x1x2)^2
=23^2-2*(-7)^2
=23^2-2*49=431
D=9x1x2+3(x1^2+x2^2)+x1x2
=10x1x2+3*23
=69+10*(-7)=-1
18 tháng 8 2021
6: \(-x^2y\left(xy^2-\dfrac{1}{2}xy+\dfrac{3}{4}x^2y^2\right)\)
\(=-x^3y^3+\dfrac{1}{2}x^3y^2-\dfrac{3}{4}x^4y^3\)
7: \(\dfrac{2}{3}x^2y\cdot\left(3xy-x^2+y\right)\)
\(=2x^3y^2-\dfrac{2}{3}x^4y+\dfrac{2}{3}x^2y^2\)
8: \(-\dfrac{1}{2}xy\left(4x^3-5xy+2x\right)\)
\(=-2x^4y+\dfrac{5}{2}x^2y^2-x^2y\)
19 tháng 8 2021
9: \(2x^2\left(x^2+3x+\dfrac{1}{2}\right)=2x^4+6x^3+x^2\)
10: \(-\dfrac{3}{2}x^4y^2\left(6x^4-\dfrac{10}{9}x^2y^3-y^5\right)\)
\(=-9x^8y^2+\dfrac{5}{3}x^6y^5+\dfrac{3}{2}x^4y^7\)
11: \(\dfrac{2}{3}x^3\left(x+x^2-\dfrac{3}{4}x^5\right)=\dfrac{2}{3}x^3+\dfrac{2}{3}x^5-\dfrac{1}{2}x^8\)
12: \(2xy^2\left(xy+3x^2y-\dfrac{2}{3}xy^3\right)=2x^2y^3+6x^3y^3-\dfrac{4}{3}x^2y^5\)
13: \(3x\left(2x^3-\dfrac{1}{3}x^2-4x\right)=6x^4-x^3-12x^2\)
CM
9 tháng 9 2017
+ 2x2 + y2 – 8x + 2y – 1 = 0 không phải phương trình đường tròn vì hệ số của x2 khác hệ số của y2.
+ Phương trình x2 + y2 + 2x – 4y – 4 = 0 có :
a = –1; b = 2; c = –4 ⇒ a2 + b2 – c = 9 > 0
⇒ phương trình trên là phương trình đường tròn.
+ Phương trình x2 + y2 – 2x – 6y + 20 = 0 có :
a = 1; b = 3; c = 20 ⇒ a2 + b2 – c = –10 < 0
⇒ phương trình trên không là phương trình đường tròn.
+ Phương trình x2 + y2 + 6x + 2y + 10 = 0 có :
a = –3; b = –1; c = 10 ⇒ a2 + b2 – c = 0 = 0
⇒ phương trình trên không là phương trình đường tròn.
CM
16 tháng 6 2017
Ta xét các phương án:
(I) có:
(II) có:
(III) tương đương : x2+ y2 – 2x - 3y + 0,5= 0.
phương trình này có:
Vậy chỉ (I) và (III) là phương trình đường tròn.
Chọn D.
15 tháng 5 2018
ta có:
x4-8x2-9=0
x4+9x2-x2-9=0
x4-x2+9x2-9=0
x2(x2-1)+9(x2-10=0
(x2-1)(x2+9)=0
=>x2-1=0=>x=1
=>x2+9=0=>x=-3
CM
9 tháng 8 2019
Đáp án D
Cách giải: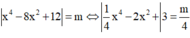 
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y = 1 4 x 4 - 2 x 2 + 3
và đường thẳng y = m 4
Từ đồ thị hàm số y = 1 4 x 4 - 2 x 2 + 3 ta suy ra đồ thị hàm số y = 1 4 x 4 - 2 x 2 + 3 có hình dạng như sau:
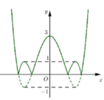
Dựa vào đồ thị hàm số ta thấy để đường thẳng y = m 4 cắt đồ thị hàm số y = 1 4 x 4 - 2 x 2 + 3 tại 8 điểm phân biệt
