Cho tam giác ABC. M là ddieeme nằm trên tia phân giác ngoài của góc C. Chứng minh rằng MA+MB>CA+CB
GIÚP MÌNH VS Ạ. CẢM ƠN !
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)
Xét∆BCM = ∆ICM ( c-g-c )
=) BM=MI
b)
Ta có BM=MI
=) MA+MB=MA+MI . (1)
Lai có BC=IC
=) AC+BC = AC+IC=AI . (2)
Xét∆AMI có AM+MI>AI ( bđt ∆ ). (3)
Từ (1);(2);(3)=) MA+MB>AC+BC

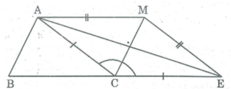
Trên tia đối tia CB lấy điểm E sao cho CE = CA. Nối MA, ME nên ∆ ACE cân tại C có CM là đường phân giác nên CM là đường trung trực (tính chất tam giác cân)
⇒ MA = ME (tính chất đường trung trực)
Ta có: AC + BC = CE + BC = BE (1)
MA + MB = ME + MB (2)
Trong ∆ MBE, ta có: BE < MB+ ME (bất đẳng thức tam giác) (3)
Từ (1), (2) và (3) suy ra: AC + CB < AM + MB.

cái này người ta thường gọi là "đã ngu còn tỏ ra nguy hiểm". Tiếng anh đã ngu rồi lại cứ thích nói tiếng anh

a: góc ABH=90-65=25 độ
b: Xét ΔCBD có
CH vừa là đường cao, vừa là trung tuyến
nên ΔCBD cân tại C
=>CH là phân giác của góc BCD