Cho đường thẳng (d): y = mx + 5 ; (P): y =x2
Tìm m để (d) cắt (P) tại 2 điểm phân biệt có hoành độ lần lượt là x1, x2 với x1 < x2 ; |x1| > |x2|
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì (Δ) // (d) \(\Rightarrow\left\{{}\begin{matrix}m=-2\\n\ne5\end{matrix}\right.\) \(\Rightarrow\left(\Delta\right):y=-2x+n\)
Phương trình hoành độ giao điểm của (Δ) và (P)
\(-2x+n=-\dfrac{1}{2}x^2\) \(\Leftrightarrow\dfrac{1}{2}x^2-2x+n=0\) (*)
Ta có: \(\Delta'=1-\dfrac{1}{2}n\)
Để (Δ) và (P) có 1 điểm chung duy nhất
\(\Leftrightarrow\) Phương trình (*) có nghiệm kép \(\Leftrightarrow1-\dfrac{1}{2}n=0\) \(\Leftrightarrow n=2\) (Thỏa mãn)
Vậy \(m=-2\) và \(n=2\)

- Xét đường tròn \(\left(C\right)\) có tâm \(I\left(1;0\right)\) và \(R=\dfrac{\sqrt{5}}{5}\)
- Để đường thẳng d và đường tròn không có điểm chung
\(\Leftrightarrow d_{\left(d/I\right)}=\dfrac{\left|m-2m+3\right|}{\sqrt{m^2+1}}>R=\dfrac{\sqrt{5}}{5}\)
\(\Leftrightarrow\dfrac{m^2-6m+9}{m^2+1}>\dfrac{1}{5}\)
\(\Leftrightarrow\dfrac{m^2-6m+9-0,2m^2-0,2}{m^2+1}>0\)
\(\Leftrightarrow0,8m^2-6m+8,8>0\)
\(\Leftrightarrow\left[{}\begin{matrix}m>2\\m< \dfrac{11}{2}\end{matrix}\right.\)
Vậy ...
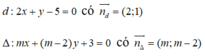
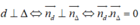
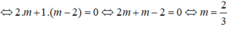


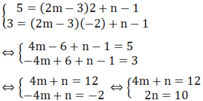
PTHĐGĐ là:
x^2-mx-5=0
a=1; b=-m; c=-5
Vì ac<0 nên (d) luôn cắt (P) tại hai điểm phân biệt
x1<x2; |x1|>|x2|
=>x1<0; x2>0
=>x1*x2<0
=>Luôn đúng