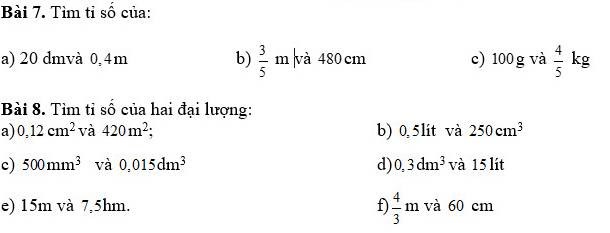
giúp mình vs mình cảm ơn nhiều
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
AH
Akai Haruma
Giáo viên
6 tháng 9 2021
Câu 4a.
Kẻ tia $Om\parallel Ax$ như hình:
Vì $Ax\parallel Om$ nên $\widehat{AOm}=\widehat{xAO}=30^0$ (hai góc so le trong)
$\Rightarrow \widehat{mOB}=\widehat{AOB}-\widehat{AOm}=70^0-30^0=40^0$
$Ax\parallel By, Ax\parallel Om\Rightarrow By\parallel Om$
$\Rightarrow \widehat{B}=\widehat{mOB}=40^0$ (hai góc so le trong)
6 tháng 9 2021
a) Trên nửa mặt phẳng bờ OB chứa điểm A, kẻ tia Oz//Ax//By
Ta có: Oz//Ax(cách vẽ)
\(\Rightarrow\widehat{xAO}=\widehat{AOz}=30^0\)( 2 góc so le trong)
Ta có: \(\widehat{AOz}+\widehat{zOB}=\widehat{AOB}\)
\(\Rightarrow\widehat{zOB}=\widehat{AOB}-\widehat{AOz}=70^0-30^0=40^0\)
Ta có: Oz//By
\(\Rightarrow\widehat{B}=\widehat{zOB}=40^0\)( 2 góc so le trong)
b) Xét tam giác ABC có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)( tổng 3 góc trong tam giác)
\(\Rightarrow\widehat{C}=180^0-\widehat{A}-\widehat{B}=180^0-60^0-40^0=80^0\)
\(\Rightarrow y=80^0\)
Xét tứ giác AEDB có:
\(\widehat{AED}+\widehat{EDB}+\widehat{ABD}+\widehat{BAE}=360^0\)
\(\Rightarrow\widehat{EDB}=360^0-\widehat{AED}-\widehat{ABD}-\widehat{BAE}=360^0-90^0-40^0-60^0=170^0\)
\(\Rightarrow x=170^0\)
5 tháng 7 2021
- Xét : \(x^2+8x-20\le0\)
\(\Rightarrow-10\le x\le2\)
Mà \(x>0\)
\(\Rightarrow0< x\le2\)
- Xét \(x^2-2\left(m+3\right)x+m^2-2m< 0\)
Có : \(\Delta^,=b^{,2}-ac=\left(m+3\right)^2-\left(m^2-2m\right)\)
\(=m^2+6m+9-m^2+2m=8m+9\)
- Để bất phương trình có nghiệm
\(\Leftrightarrow\Delta>0\)
\(\Leftrightarrow m>-\dfrac{9}{8}\)
=> Bất phương trình có nghiệm \(S=\left(x_1;x_2\right)\)
Mà \(0< x\le2\)
\(\Rightarrow0< x_1< x_2\le2\)
\(TH1:x=2\)
\(\Rightarrow4-4\left(m+3\right)+m^2-2m< 0\)
\(\Rightarrow3-\sqrt{17}< m< 3+\sqrt{17}\)
\(TH2:0< x_1< x_2< 2\)
\(\Rightarrow\left\{{}\begin{matrix}m^2-2m>0\\m^2-6m-8>0\\0< 2\left(m+3\right)< 2\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}m< 0\\m>2\end{matrix}\right.\\\left[{}\begin{matrix}m>3+\sqrt{17}\\m< 3-\sqrt{17}\end{matrix}\right.\\-3< m< -2\end{matrix}\right.\)
Vậy \(3-\sqrt{7}< m< 3+\sqrt{7}\)
6 tháng 7 2021
Ban ơi :(( ngay chỗ dấu ngoặc nhọn đầu tiên của TH2 có công thức j k bạn?
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 7 2021
Nếu \(y\le0\Rightarrow\left(y-4\right)^2\ge16>9\left(ktm\right)\Rightarrow y>0\)
Nếu \(x\ge0\Rightarrow\left(x+5\right)^2\ge25>9\left(ktm\right)\Rightarrow x< 0\)
Đặt \(\left\{{}\begin{matrix}-x=a>0\\y=b>0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left(a-5\right)^2+\left(b-4\right)^2\le9\\3a+b\ge14\end{matrix}\right.\)
Ta có:
\(14^2\le\left(3a+b\right)^2\le\left(3^2+1\right)\left(a^2+b^2\right)\Rightarrow a^2+b^2\ge\dfrac{196}{10}=\dfrac{98}{5}\)
\(P_{min}=\dfrac{98}{5}\) khi \(\left(a;b\right)=\left(\dfrac{21}{5};\dfrac{7}{5}\right)\) hay \(\left(x;y\right)=\left(-\dfrac{21}{5};\dfrac{7}{3}\right)\)
Lại có:
\(\left(a-5\right)^2+\left(b-4\right)^2\le9\Leftrightarrow a^2+b^2\le10a+8b-32\le\sqrt{\left(10^2+8^2\right)\left(a^2+b^2\right)}-32\)
\(\Rightarrow P\le2\sqrt{41}\sqrt{P}-32\Leftrightarrow P-2\sqrt{41}\sqrt{P}+32\le0\)
\(\Rightarrow\left(\sqrt{P}-3-\sqrt{41}\right)\left(\sqrt{P}-3+\sqrt{41}\right)\le0\) (1)
Do \(P\ge\dfrac{98}{5}\Rightarrow\sqrt{P}-3+\sqrt{41}>0\)
Nên (1) tương đương: \(\sqrt{P}-3-\sqrt{41}\le0\Rightarrow P\le50+6\sqrt{41}\)
\(P_{max}=50+6\sqrt{41}\) khi \(\left(a;b\right)=\left(5+\dfrac{15}{\sqrt{41}};4+\dfrac{12}{\sqrt{41}}\right)\)
mn giúp mình bài 3 vs ạ. Mình cảm ơn nhiều
5 tháng 7 2021
Xét pt hoành độ gđ của đường thẳng và parabol có:
\(\left(m-1\right)x^2+3mx+2m=2x-1\)
\(\Leftrightarrow\left(m-1\right)x^2+x\left(3m-2\right)+2m+1=0\) (1)
Để đt và parabol cắt tại hai điểm pb có hoành độ âm
\(\Leftrightarrow\) Pt (1) có hai nghiệm âm phân biệt
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\S< 0\\P>0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m^2-8m+8>0\\\dfrac{2-3m}{m-1}< 0\\\dfrac{2m+1}{m-1}>0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m\in\left(-\infty;4-2\sqrt{2}\right)\cup\left(4+2\sqrt{2};+\infty\right)\\m\in\left(-\infty;\dfrac{2}{3}\right)\cup\left(1;+\infty\right)\\m\in\left(-\infty;-\dfrac{1}{2}\right)\cup\left(1;+\infty\right)\end{matrix}\right.\)
\(\Rightarrow m\in\left(-\infty;-\dfrac{1}{2}\right)\cup\left(4+2\sqrt{2};+\infty\right)\)
Vậy...
TT
1
KY
9 tháng 9 2021
Refer
1. “Your cousin speaks English very well” Paul told me
Paul said that ___________my cousin spoke English very well____________
2. “The man broke out of prison yesterday” said the policeman
The policeman told us_that the man had broken out of prison the day beforr__
3. “I’ll lend you this book as soon as I finish it” Owen said to me
Owen said __me that he would lend me that book as soon as he finished it___
4. “I think I forgot to turn off the lights this morning” Brenda told Brian
Brenda told Brian ____that he thought he had forgotten to turn off the lights that morning.____
5. “I work eight hours a day, except when the children are on holiday” said Mrs. Wood
Mrs. Wood said me that he worked eight hours a day, excepted when the children were on holiday
6. “You’ve been making good progress this semester” Miss Lynn told me
Miss Lynn said that _____I had been making good progress that semester_________
7. “If you bought all the tickets, you would win the lottery” the man said
The man told me ______that If I had bought all the tickets, I would win the lottery______________
8. “I like swimming but I don’t go very often” Jill said to Pam
Jill said that ______he liked swimming but he didn’t go very often___________________________
9. “I want to buy it, but I haven’t brought any money” said Patrick
Patrick told me _________that he wanted to buy it, but he hadn’t brought any money_______________________
10. “I’m going to visit my aunt in Hue, but I’m not sure when” said Mai
Mai told me _________that she was going to visit her aunt in Hue, but she was not sure when__________________
TH
0
LB
1
13 tháng 8 2021
18.\(\)\(=>I1=\dfrac{U}{R1}=\dfrac{16}{4R2}=\dfrac{4}{R2}A,\)
\(=>I2=\dfrac{U}{R2}=\dfrac{16}{R2}\left(A\right)\)
\(=>I2=I1+6< =>\dfrac{16}{R2}=\dfrac{4}{R2}+6< =>R2=2\left(ôm\right)\)
\(=>I1=\dfrac{4}{2}=2A,=>I2=2+6=8A\)
\(=>R1=4R2=8\left(ôm\right)\)
19
\(I2=1,5I1< =>\dfrac{U}{R2}=\dfrac{1,5U}{R1}=>\dfrac{1}{R2}=\dfrac{1,5}{R1}\)
\(< =>\dfrac{1}{R2}=\dfrac{1,5}{R2+5}=>R2=10\left(ôm\right)=>R1=R2+5=15\left(ôm\right)\)
7:
a: 0,4m=40dm
=>Tỉ số là 20/40=1/2
b: 3/5m=60cm
=>tỉ số là 60/480=1/8
c: 4/5kg=800g
=>Tỉ số là 100/800=1/8
7:
a: 0,4m=40dm
=>Tỉ số là 20/40=1/2
b: 3/5m=60cm
=>tỉ số là 60/480=1/8
c: 4/5kg=800g
=>Tỉ số là 100/800=1/8