gảii giúp mk vớii
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(\dfrac{3}{n\left(n+3\right)}=\dfrac{\left(n+3\right)-n}{n\left(n+3\right)}=\dfrac{n+3}{n\left(n+3\right)}-\dfrac{n}{n\left(n+3\right)}=\dfrac{1}{n}-\dfrac{1}{n+3}\)
Do đó:
\(C=\dfrac{1}{1}-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+..+\dfrac{1}{37}-\dfrac{1}{40}\)
\(=1-\dfrac{1}{40}=\dfrac{39}{40}\)


a: \(\widehat{xOm};\widehat{nOm}\)
\(\widehat{nOm};\widehat{yOn}\)
\(\widehat{yOn};\widehat{xOn}\)
\(\widehat{xOm};\widehat{yOm}\)
b: \(\widehat{yOn};\widehat{xOn}\)
\(\widehat{xOm};\widehat{yOm}\)
c: \(\widehat{mOy}=180^0-30^0=150^0\)
\(\widehat{nOx}=180^0-50^0=130^0\)
\(\widehat{mOn}=180^0-80^0=100^0\)

\(\left\{{}\begin{matrix}\overrightarrow{AB}=\left(4;-7\right)\\\overrightarrow{BC}=\left(4;8\right)\\\overrightarrow{AC}=\left(8;1\right)\end{matrix}\right.\) \(\Rightarrow\overrightarrow{BC}+\overrightarrow{AC}=\left(12,9\right)\)
\(\Rightarrow\overrightarrow{AB}.\left(\overrightarrow{BC}+\overrightarrow{AC}\right)=4.12-7.9=...\)
b. Gọi \(H\left(x;y\right)\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AH}=\left(x+3;y-5\right)\\\overrightarrow{BH}=\left(x-1;y+2\right)\\\end{matrix}\right.\)
Do \(AH\perp BC\Rightarrow\overrightarrow{AH}.\overrightarrow{BC}=0\)
\(\Rightarrow4\left(x+3\right)+8\left(y-5\right)=0\)
\(\Rightarrow x+2y=7\) (1)
Do H thuộc BC \(\Rightarrow\dfrac{x-1}{4}=\dfrac{y+2}{8}\Rightarrow2x-y=4\Rightarrow y=2x-4\)
Thế vào (1) \(\Rightarrow x+2\left(2x-4\right)=7\Rightarrow x=3\Rightarrow y=2\)
\(\Rightarrow H\left(3;2\right)\)


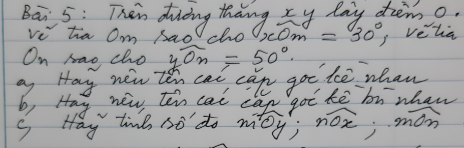 giúp em vớii
giúp em vớii



Lời giải:
a) Xét tam giác $ADB$ và $AEC$ có:
$\widehat{A}$ chung
$\widehat{ADB}=\widehat{AEC}=90^0$
$\Rightarrow \triangle ADB\sim \triangle AEC$ (g.g)
(đpcm)
b) Xét tam giác $EHB$ và $DHC$ có:
$\widehat{EHB}=\widehat{DHC}$ (đối đỉnh)
$\widehat{HEB}=\widehat{HDC}=90^0$
$\Rightarrow \triange EHB\sim \triangle DHC$ (g.g)
$\Rightarrow \frac{EH}{DH}=\frac{HB}{HC}$
$\Rightarrow HE.HC=HD.HB$ (đpcm)
Hình vẽ: