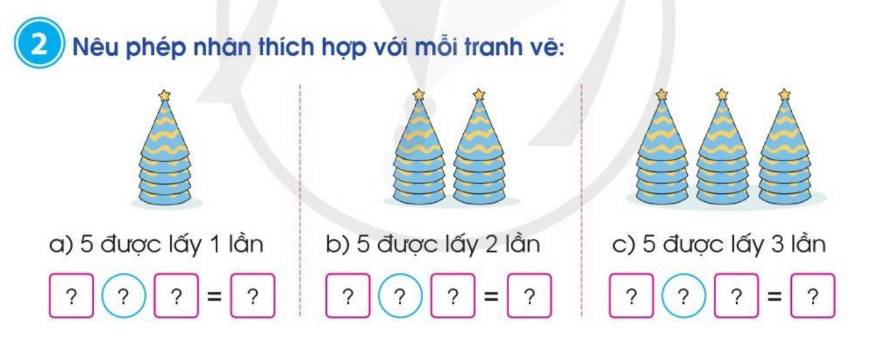
Nêu phép nhân thích hợp với mỗi tranh vẽ:a, 5 được lấy 1 lầnb, 5 được lấy 2 lầnc, 5 được lấy 3...
Đọc tiếp
Nêu phép nhân thích hợp với mỗi tranh vẽ:
a, 5 được lấy 1 lần
b, 5 được lấy 2 lần
c, 5 được lấy 3 lần
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
4
CM
3 tháng 2 2019
Không gian mẫu là năm lần lấy ngẫu nhiên từ mỗi hộp ra 2 cái bánh.
Suy ra số phần tử của không gian mẫu là 
.
Gọi A là biến cố Trong năm lần lấy ra có bốn lần lấy được 2 bánh mặn và một lần lấy được 2 bánh ngọt . Ta mô tả không gian của biến cố A như sau:
● Giai đoạn thứ nhất. Chọn 4 hộp bánh từ 5 hộp bánh, có 
cách. Sau đó mỗi hộp chọn ra 2 bánh mặn, có 
cách. Do đó có tất cả 
cách cho giai đoạn này.
● Giai đoạn thứ hai. Hộp còn lại duy nhất chọn ra 2 bánh ngọt nên có 
cách.
Suy ra số phần tử của biến cố A là 
Vậy xác suất cần tính
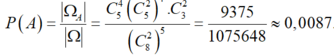
Chọn C.
CM
20 tháng 9 2019
Giả sử tuổi bạn là x. Đem tuổi của mình:
+ Cộng thêm 5 ⇒ x + 5
+ Được bao nhiêu đem nhân với 2 ⇒ (x + 5).2
+ Lấy kết quả trên cộng với 10 ⇒ (x + 5).2 + 10
+ Nhân kết quả vừa tìm được với 5 ⇒ [(x + 5).2 + 10].5
+ Đọc kết quả cuối cùng sau khi đã trừ đi 100 ⇒ [(x + 5).2 + 10].5 – 100
Rút gọn biểu thức trên :
[(x + 5).2 + 10].5 – 100
= (x.2 + 5.2 + 10).5 – 100
= (2x + 20).5 – 100
= 2x.5 + 20.5 – 100
= 10x + 100 – 100
= 10x
Vậy kết quả cuối cùng bằng mười lần số tuổi thực của bạn. Do đó ta chỉ cần lấy kết quả cuối cùng chia cho 10 là ra số tuổi thực.
11 tháng 8 2021
Gọi số đó là a
Ta có:
\(\left\{\left[\left(8a+1\right)\frac{4}{7}+\frac{1}{2}\right]-\frac{1}{2}\right\}:3+\frac{1}{2}=0,6\)
\(\left\{\left[\left(8a+1\right)\frac{4}{7}+\frac{1}{2}\right]-\frac{1}{2}\right\}:3=\frac{1}{5}\)
\(\left[\left(8a+1\right)\frac{4}{7}+\frac{1}{2}\right]-\frac{1}{2}=\frac{1}{15}\)
\(\left(8a+1\right)\frac{4}{7}+\frac{1}{2}=\frac{17}{30}\)
\(\left(8a+1\right)\frac{4}{7}=\frac{1}{15}\)
\(8a+1=\frac{7}{45}\)
\(8a=\frac{-38}{45}\)
\(a=\frac{-19}{180}\)
\(\left\{\left[\left(8a+1\right)\frac{4}{7}+\frac{1}{2}\right]-\frac{1}{2}\right\}:3=\frac{1}{5}\)
a: 5*1=5
b: 5*2=10
c: 5*3=15