Tìm nghiệm của đa thức sau:
a) x2 - 20x - 300
b) 2x2 + 35x + 33
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
C
14 tháng 3 2023
`x^2 - 3x = 0`
`<=> x.(x-3)=0`
`<=> x = 0` hoặc `x-3=0`
`<=> x = 0 ` hoặc `x = 3`
Vậy `S = { 0;3}`
`2x^2 + 5x = 0`
`<=> x.(2x + 5)=0`
`<=> x = 0` hoặc `2x+5=0`
`<=> x = 0` hoặc `2x= -5`
`<=> x = 0` hoặc `x = -5/2`
Vậy `S = {0; -5/2}`
14 tháng 3 2023
\(a,x^2-3x=0\\ x\left(x-3\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=0\\x-3=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=3\end{matrix}\right.\\ b,2x^2+5x=0\\ x\left(2x+5\right)=0\\ \Rightarrow\left[{}\begin{matrix}x=0\\2x+5=0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{5}{2}\end{matrix}\right.\)
18 tháng 3 2022
a. cậu thu gọn bằng cách dùng t/c kết hợp và giao hoán
b. cậu thay từng giá vào biểu thức vừa được rút gọn để tìm
c. thì.... tớ ko biết
KK
3
NT
Nguyễn thành Đạt
CTVHS
11 tháng 4 2023
Phân tích đa thức thành nhân tử thôi bạn :
Ta có :
\(h\left(x\right)=x^2+5x+6\)
\(h\left(x\right)=x\left(x+2\right)+3\left(x+2\right)\)
\(h\left(x\right)=\left(x+2\right)\left(x+3\right)\)
\(\Rightarrow N_oh\left(x\right)=-2;-3\)
\(g\left(x\right)=2x^2+7x-9\)
\(g\left(x\right)=2x^2+9x-2x-9\)
\(g\left(x\right)=2x\left(x-1\right)+9\left(x-1\right)\)
\(g\left(x\right)=\left(x-1\right)\left(2x+9\right)\)
\(\Rightarrow N_og\left(x\right)=1;-4,5\)
CM
4 tháng 1 2018
c. Ta có h(x) = 0 ⇒ 5x + 1 = 0 ⇒ x = -1/5
Vậy nghiệm của đa thức h(x) là x = -1/5 (1 điểm)
12 tháng 3 2022
Bài 2 :
a, \(x^2-4x+4+1=\left(x-2\right)^2+1\ge1\)
Dấu ''='' xảy ra khi x = 2
b, Ta có \(\left(x+1\right)^2+10\ge10\Rightarrow\dfrac{-100}{\left(x+1\right)^2+10}\ge-\dfrac{100}{10}=-10\)
Dấu ''='' xảy ra khi x = -1
12 tháng 3 2022
Bài 1 :
a, Ta có \(A\left(x\right)=x^2-4x+4=0\Leftrightarrow\left(x-2\right)^2=0\Leftrightarrow x=2\)
b, \(B\left(x\right)=x^2\left(2x+1\right)+\left(2x+1\right)=\left(x^2+1>0\right)\left(2x+1\right)=0\Leftrightarrow x=-\dfrac{1}{2}\)
c, \(C\left(x\right)=\left|2x-3\right|=\dfrac{1}{3}\Leftrightarrow\left[{}\begin{matrix}2x=\dfrac{1}{3}+3=\dfrac{10}{3}\\2x=-\dfrac{1}{3}+3=\dfrac{8}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{3}\\x=\dfrac{4}{3}\end{matrix}\right.\)
NP
1
4 tháng 3 2022
a, Cho \(x^2+2022x=0\Leftrightarrow x\left(x+2022\right)=0\Leftrightarrow x=0;x=-2022\)
b, \(3x^2+7x+4=0\Leftrightarrow\left(x+1\right)\left(3x+4\right)=0\Leftrightarrow x=-1;x=-\dfrac{4}{3}\)
c, \(2\left(x^2+2x+1-1\right)+5=0\Leftrightarrow2\left(x+1\right)^2+3=0\)(vô lí)
Vậy đa thức ko có nghiệm tm
AH
Akai Haruma
Giáo viên
30 tháng 4 2022
Bài 1:
1.
$6x^3-2x^2=0$
$2x^2(3x-1)=0$
$\Rightarrow 2x^2=0$ hoặc $3x-1=0$
$\Rightarrow x=0$ hoặc $x=\frac{1}{3}$
Đây chính là 2 nghiệm của đa thức
2.
$|3x+7|\geq 0$
$|2x^2-2|\geq 0$
Để tổng 2 số bằng $0$ thì: $|3x+7|=|2x^2-2|=0$
$\Rightarrow x=\frac{-7}{3}$ và $x=\pm 1$ (vô lý)
Vậy đa thức vô nghiệm.
AH
Akai Haruma
Giáo viên
30 tháng 4 2022
Bài 2:
1. $x^2+2x+4=(x^2+2x+1)+3=(x+1)^2+3$
Do $(x+1)^2\geq 0$ với mọi $x$ nên $x^2+2x+4=(x+1)^2+3\geq 3>0$ với mọi $x$
$\Rightarrow x^2+2x+4\neq 0$ với mọi $x$
Do đó đa thức vô nghiệm
2.
$3x^2-x+5=2x^2+(x^2-x+\frac{1}{4})+\frac{19}{4}$
$=2x^2+(x-\frac{1}{2})^2+\frac{19}{4}\geq 0+0+\frac{19}{4}>0$ với mọi $x$
Vậy đa thức khác 0 với mọi $x$
Do đó đa thức không có nghiệm.
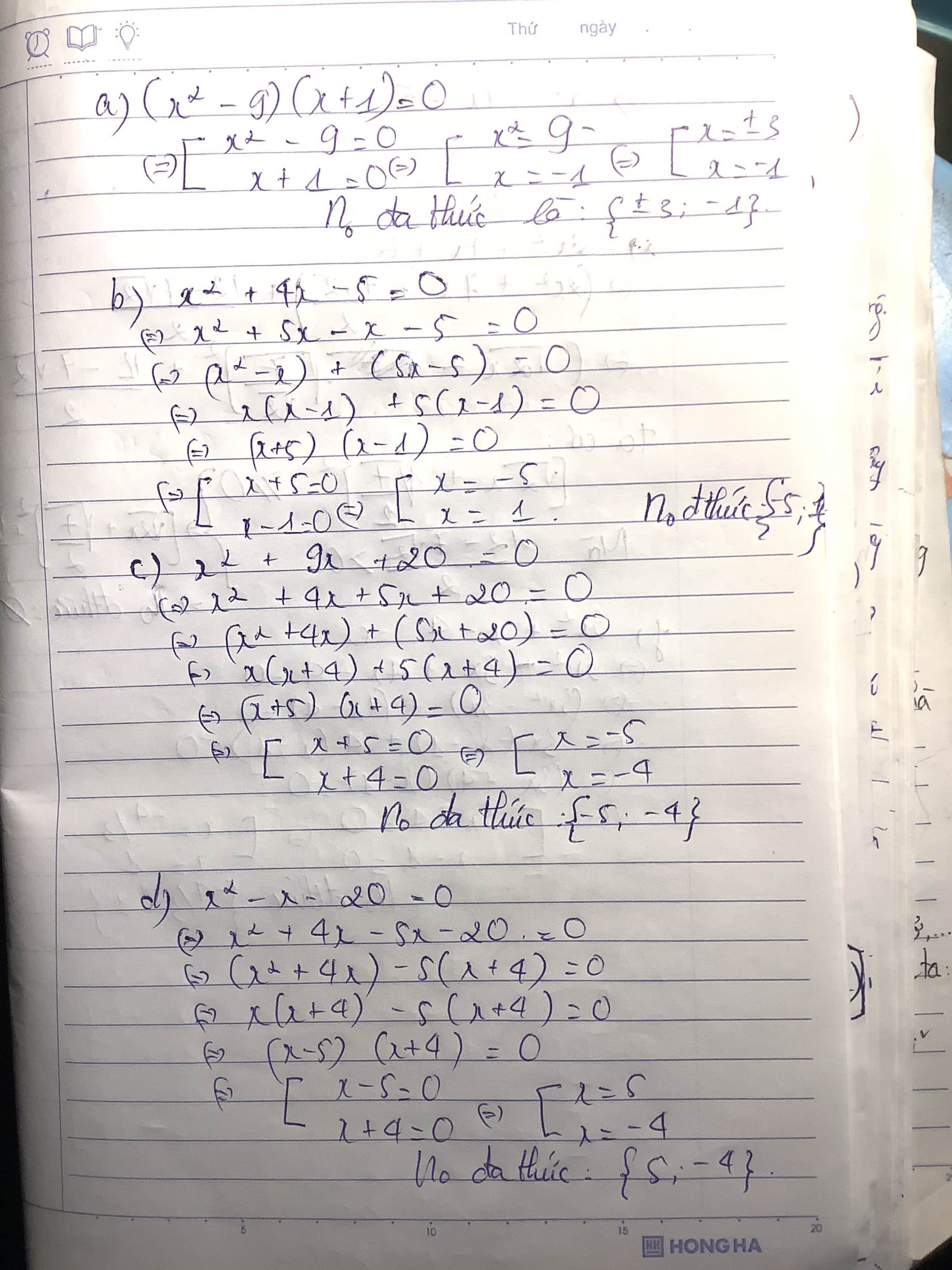
a: Đặt x^2-20x-300=0
=>x^2-30x+10x-300=0
=>(x-30)(x+10)=0
=>x=30 hoặc x=-10
b: Đặt 2x^2+35x+33=0
=>(x+1)(2x+33)=0
=>x=-33/2 hoặc x=-1