Cho tam giác ABC(3 góc nhọn) có AD và BE là đường cao cắt nhau tại H.
a,Chứng minh tam giác AEH đồng dạng với tam giác BDH
b,Chứng minh AH.ED=AB.HE
c,Nếu AC=5cm AC=3cm tính tỉ số DB/DH
CH cắt AB tại F Chứng minh rằng HD/AD+HE/BE+HF/CF=1
P/s:chỉ cần làm c d thôi nhé




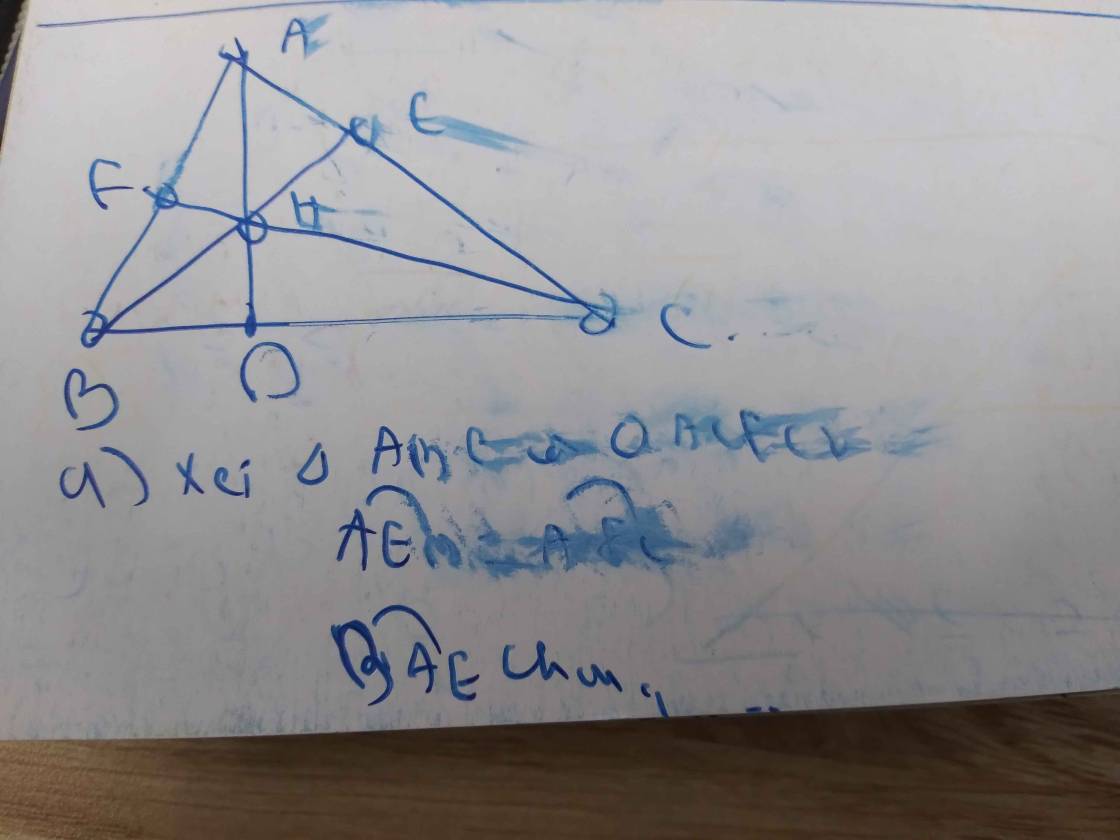

a) Xét ΔAEH vuông tại E và ΔBDH vuông tại D có
\(\widehat{AHE}=\widehat{BHD}\)(hai góc đối đỉnh)
Do đó: ΔAEH\(\sim\)ΔBDH(g-g)