cho cho hai đa thưc P(x)=-x^3+2x^2 +x-1 và Q(x)=x^3-x^2-x+2.ngiệm của đa thức P(x)+Q(x) là :
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Ta có : \(P\left(x\right)=5x^3-3x+7-x=5x^3-4x+7\)
\(Q\left(x\right)=5x^3+2x-3+2x-x^2-2=5x^3-x^2+4x-5\)
b, Ta có : \(M\left(x\right)=P\left(x\right)+Q\left(x\right)\)
hay \(5x^3-4x+7+5x^3-x^2+4x-5=10x^3-x^2+2\)
Ta có ; \(N\left(x\right)=P\left(x\right)-Q\left(x\right)\)
hay \(5x^3-4x+7-5x^3+x^2-4x+5=x^2-8x+12\)
c, phải là tìm nghiệm N(x) chứ ?

a, P(x)=5x3+x2-3x+7
Q(x)=-5x3-x2+4x-5(đã thu gọn-bn tự trình bày nha)
b,P(x)=5x3+x2-3x+7
+
Q(x)=-5x3-x2+4x-5
M(x)= x-2
P(x)= 5x3 +x2 -3x+7
-
Q(x)=-5x3 - x2 + 4x-5
N(x)=10x3+2x2-7x+12
c, x-2=0
x=0+2
x=2
=>Nghiệm bằng 2.

`Q(x)=-5x^3+2x-3+2x-x^2-2`
`=-5x^3+4x-5`
`M(x)=P(x)+Q(x)`
`=5x^3-3x+7-5x^3+4x-5`
`=x+2`
`N(x)=P(x)-Q(x)`
`=5x^3-3x+7+5x^3-4x+5`
`=10x^3-7x+12`
b)Đặt `M(x)=0`
`<=>x+2=0`
`<=>x=-2`
Vậy M(x) có nghiệm `x=-2`
1k like đâu ![]()
a) \(P\left(x\right)=5x^3-3x+7-x\\ =5x^3+\left(-3x-x\right)+7\\ =5x^3-4x+7\\ Q\left(x\right)=-5x^3+2x-3+2x-x^2-2\\ =-5x^3+\left(2x+2x\right)+\left(-3-2\right)+x^2\\ =-5x^3+4x-5+x^2\)
\(M\left(x\right)=P\left(x\right)+Q\left(x\right)\\ =5x^3-4x+7+\left(-5x^3\right)+4x-5-x^2\\ =\left(5x^3-5x^3\right)+\left(-4x+4x\right)+\left(7-5\right)-x^2\\ =2-x^2\\ N\left(x\right)=P\left(x\right)-Q\left(x\right)\\ =5x^3-4x+7-\left(-5x^3+4x-5+x^2\right)\\ =5x^3-4x+7+5x^3-4x+5-x^2\\ =\left(5x^3+5x^3\right)+\left(-4x-4x\right)+\left(7+5\right)+x^{^2}\\ =10x^3-8x+12+x^2\)

` P(x) = x^3-2x^2+x-2`
`Q(x) = 2x^3 - 4x^2+ 3x – 56`
a) `P(x) -Q(x)`
`= x^3-2x^2+x-2 - 2x^3 +4x^2 -3x +56`
`=(x^3-2x^3) +(4x^2-2x^2) +(x-3x) +(-2+56)`
`= -x^2 +2x^2 -2x +54`
b) Thay `x=2` vào `P(x)` ta đc
`P(2) = 2^3 -2*2^2 +2-2`
`= 8-8+2-2 =0`
Vậy chứng tỏ `x=2` là nghiệm của đa thức `P(x)`
Thay `x=2` vào `Q(x)` ta đc
`Q(2) = 2*2^3 -4*2^2 +3*2-56`
`=16 -16+6-56`
`= -50`
Vậy chứng tỏ `x=2` là ko nghiệm của đa thức `Q(x)`

cho mình hỏi chút có ai chơi free fire nếu có nhắn mình nha thanhk bạn
a, Ta có : \(P\left(x\right)+Q\left(x\right)\)ta được :
\(2x^3-3x^2+x+x^3-x^2+2x+1=3x^3-3x^2+3x+1\)
b, \(P\left(x\right)+M\left(x\right)=2Q\left(x\right)\Rightarrow M\left(x\right)=2Q\left(x\right)-P\left(x\right)\)
\(M\left(x\right)=2x^3-2x^2+4x+2-2x^3+3x^2-x=x^2+3x+2\)
c, Thay x = -2 vào đa thức M(x) ta được :
\(4-6+2=0\)* đúng *
Vậy x = -2 là nghiệm của đa thức M(x)

a: \(P\left(x\right)=5x^3-4x+7\)
\(Q\left(x\right)=-5x^3-x^2+4x-5\)
b: \(M\left(x\right)=-x^2+2\)
\(N\left(x\right)=10x^3+x^2-8x+12\)
c: Đặt M(x)=0
=>2-x2=0
hay \(x\in\left\{\sqrt{2};-\sqrt{2}\right\}\)

a: \(P\left(x\right)=3x^2-x-1\)
\(Q\left(x\right)=-3x^2-4x-2\)
b: \(G\left(x\right)=3x^2-x-1+3x^2+4x+2=6x^2+3x+1\)
c: Để G(x)-6x-1=0 thì 6x2-3x=0
=>3x(2x-1)=0
=>x=0 hoặc x=1/2

`a,`
`P(x)=5x^3 - 3x + 7 - x`
`= 5x^3 +(-3x-x)+7`
`= 5x^3-4x+7`
Bậc: `3`
`Q(x)=-5x^3 + 2x - 3 + 2x - x^2 - 2`
`= -5x^3-x^2+(2x+2x)+(-3-2)`
`= -5x^3-x^2+4x-5`
Bậc: `3`
`b,`
`P(x)=M(x)-Q(x)`
`-> M(x)=P(x)+Q(x)`
`M(x)=(5x^3-4x+7)+(-5x^3-x^2+4x-5)`
`M(x)=5x^3-4x+7-5x^3-x^2+4x-5`
`M(x)=(5x^3-5x^3)-x^2+(-4x+4x)+(7-5)`
`M(x)=-x^2+2`
`c,`
`M(x)=-x^2+2=0`
`\leftrightarrow -x^2=0-2`
`\leftrightarrow -x^2=-2`
`\leftrightarrow x^2=2`
`\leftrightarrow `\(\left[{}\begin{matrix}x=\sqrt{2}\\x=-\sqrt{2}\end{matrix}\right.\)
Vậy, nghiệm của đa thức là \(x=\left\{\sqrt{2};-\sqrt{2}\right\}\)

a, \(P\left(x\right)=5x^3-3x+7-x\)
\(=5x^3-4x+7\)
\(Q\left(x\right)=-5x^3+2x-3+2x-x^2-2\)
\(=-5x^3-x^2+4x-5\)
Ta có \(P\left(x\right)+Q\left(x\right)=-x^2+2\)
\(P\left(x\right)-Q\left(x\right)=10x^3+x^2-8x+12\)
b, \(P\left(x\right)+Q\left(x\right)=0\)
\(\Leftrightarrow-x^2+2=0\)
\(\Leftrightarrow-x^2=-2\)
\(\Leftrightarrow x^2=2=\left(\pm\sqrt{2}\right)^2\)
\(\Rightarrow x=\pm\sqrt{2}\)
Vậy \(x=\pm\sqrt{2}\)
P(x) = 5x3 - 3x + 7 - x
= 5x3 - 4x + 7
Q(x) = -5x3 + 2x - 3 + 2x - x2 - 2
= -5x3 - x2 + 4x - 5
P(x) + Q(x) = ( 5x3 - 4x + 7 ) + ( -5x3 - x2 + 4x - 5 )
= 5x3 - 4x + 7 - 5x3 - x2 + 4x - 5
= -x2 + 2
P(x) - Q(x) = ( 5x3 - 4x + 7 ) - ( -5x3 - x2 + 4x - 5 )
= 5x3 - 4x + 7 + 5x3 + x2 - 4x + 5
= 10x3 + x2 - 8x + 12
Đặt H(x) = P(x) + Q(x)
=> H(x) = -x2 + 2
H(x) = 0 <=> -x2 + 2 = 0
<=> -x2 = -2
<=> x2 = 2
<=> x = \(\pm\sqrt{2}\)
Vậy nghiệm của đa thức là \(\pm\sqrt{2}\)
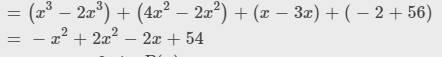
Ta có P(x)+Q(x)
=(-x^3+2x^2+x-1)+(x^3-x^2-x+2)
=-x^3+2x^2+x-1+x^3-x^2-x+2
=(-x^3+x^3)+(2x^2-x^2)+(x-x)+(-1+2)
=x^2+1
Ta có p(x)+Q(x)=0
x^2+1=0
x^2=-1(vô lí vì x^2\(\ge\)0)
Vậy đa thức P(x)+Q(x) vô nghiệm
Có P(x)+Q(x)=(-x^3+2x^2+x-1)+(x^3-x^2-x+2)
=-x^3+2x^2+x-1+x^3-x^2-x+2
=(-x^3+x^3)+(2x^2-x^2)+(x-x)+(-1+2)
=0+x^2+0+1=x^2+1
Vì x^2 \(\ge\)0 Với mọi x
=>x^2+1\(\ge\)0+1>0
=>p(x)+q(x) > 0
vậy P(x) +Q(x) ko có nghiệm