Cho hình thang ABCD (AB//CD). Gọi O là giao điểm của 2 đường chéo AC và BD. Qua O kẻ đường thẳng song song với AB, cắt AD và BC theo thứ tự E và G. a) Chứng minh OA.OD=OB.OC. b) Cho AB = 5 cm, CD= 10 cm, Oc = 6 cm. Tính OA, OE. c) Chứng minh rằng : 1/OE = 1/OG = 1/AB + 1/CD ( giúp mik với ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KT
11 tháng 5 2018
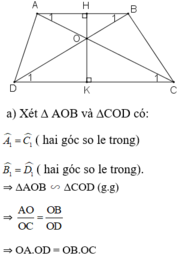
a) Xét \(\Delta OAB\)và \(\Delta OCD\)có:
\(\widehat{OAB}=\widehat{OCD}\) (slt)
\(\widehat{OBA}=\widehat{ODC}\) (slt)
suy ra: \(\Delta OAB~\Delta OCD\) (g.g)
\(\Rightarrow\)\(\frac{OA}{OC}=\frac{OB}{OD}\)
\(\Rightarrow\)\(OA.OD=OB.OC\)
b) \(\Delta OAB~\Delta OCD\)
\(\Rightarrow\)\(\frac{OA}{AC}=\frac{AB}{CD}\)
\(\Rightarrow\)\(OA=\frac{OC.AB}{CD}=3\)
\(\Rightarrow\)\(AC=OA+OC=9\)
\(\Delta AEO~\Delta ADC\) ( do OE // DC )
\(\Rightarrow\)\(\frac{OE}{DC}=\frac{OA}{AC}\) \(\Rightarrow\) \(OE=\frac{OA.DC}{AC}=\frac{10}{3}\)
28 tháng 6 2020
TỰ VẼ HÌNH NHA
a) Xét ΔABO và ΔCOD có:
\(\widehat{ABO}=\widehat{COD}\left(AB//DC\right)\)
\(\widehat{AOB}=\widehat{DOC}\left(đđ\right)\)
=> \(\text{ Δ}ABO~\text{Δ}COD\left(g.g\right)\)
\(\Rightarrow\frac{OA}{OB}=\frac{OC}{OD}\)
\(\Leftrightarrow OA.OD=OB.OC\)
b) vì ΔABO~ΔCOD
=> \(\frac{DC}{OC}=\frac{AB}{OA}\)
\(\Leftrightarrow DC.OA=AB.OC\)
\(\Leftrightarrow10.OA=5.6\)
\(\Leftrightarrow OA=3\left(cm\right)\)
OE thì mk chịu
6 tháng 2 2022
c. -Xét △ADC có: OM//DC (gt).
\(\Rightarrow\dfrac{MO}{DC}=\dfrac{AO}{AC}\) (định lí Ta-let).
\(\Rightarrow\dfrac{DC}{MO}=\dfrac{AC}{AO}\)
\(\Rightarrow\dfrac{DC}{OM}-1=\dfrac{OC}{AO}\) (1).
-Xét △BDC có: ON//DC (gt).
\(\Rightarrow\dfrac{ON}{DC}=\dfrac{BO}{BD}\) (định lí Ta-let).
\(\Rightarrow\dfrac{DC}{ON}=\dfrac{BD}{BO}\)
\(\Rightarrow\dfrac{DC}{ON}-1=\dfrac{OD}{BO}\)
-Xét △ABO có: AB//DC (gt).
\(\Rightarrow\dfrac{OD}{BO}=\dfrac{OC}{OA}=\dfrac{DC}{AB}\) (3)
-Từ (1), (2),(3) suy ra:
\(\dfrac{DC}{OM}-1=\dfrac{DC}{ON}-1=\dfrac{DC}{AB}\)
\(\Rightarrow\dfrac{DC}{OM}=\dfrac{DC}{ON}=\dfrac{DC}{AB}+1=\dfrac{AB+DC}{AB}\)
\(\Rightarrow\dfrac{1}{OM}=\dfrac{1}{ON}=\dfrac{AB+DC}{AB.DC}=\dfrac{1}{AB}+\dfrac{1}{CD}\)
6 tháng 2 2022
a: Xét ΔAOB và ΔCOD có
\(\widehat{OAB}=\widehat{OCD}\)
\(\widehat{AOB}=\widehat{COD}\)
Do đó: ΔAOB∼ΔCOD
Suy ra: \(\dfrac{OA}{OC}=\dfrac{OB}{OD}=\dfrac{AB}{CD}\)
hay \(OA\cdot OD=OB\cdot OC\)
b: \(\dfrac{OA}{OC}=\dfrac{AB}{CD}\)
\(\Leftrightarrow OA=\dfrac{1}{2}\cdot6=3\left(cm\right)\)
17 tháng 3 2020
Bài 6 :
Tự vẽ hình nhá :)
a) Gọi O là giao điểm của AC và EF
Xét tam giác ADC có :
EO // DC => AE/AD = AO/AC (1)
Xét tam giác ABC có :
OF // DC
=> CF/CB = CO/CA (2)
Từ (1) và (2) => AE/AD + CF/CB = AO/AC + CO/CA = AO + CO/AC = AC/AC = 1 => đpcm
Bài 7 :
a) Do EF // AB => CF / CA = EF / AB => CF / EF = AC / AB (1)
Dựng MG // AC và M là trung điểm của cạnh BC => GM là đường trung bình của tam giác ABC => G là trung điểm của cạnh AB =>AG = BG
Do DK // GM => AD / AG = DK / GM => AD / BG = DK / GM
=> DK / AD = GM / BG = \(\frac{\frac{AC}{2}}{\frac{AB}{2}}=\frac{AC}{AB} \left(2\right)\)
Từ (1) và (2) => CF / EF = DK / AD
Mà tứ giác ADEF là hình bình hành ( vì EF // AD và DE // AF ) nên AD = È
=> CF = DK ( đpcm )
Bài 8 :
Ta có : AB = AM + MB = 11 + 8 = 19 ( cm )
Áp dụng hệ quả định lí Ta-lét vào tam giác ABC, ta có :
AM / AB = AN / AC => AM + AB / AB = AN + AC / AC => 19 + 11 / 19 = AN + 38 / 38 => 30/19 = 38 + AN / 38
=> 1140 = 19.AN + 722
=> AN = ( 1140 - 722 ) / 19 = 22 ( cm )
=> NC = 38 - 12 = 26 ( cm )
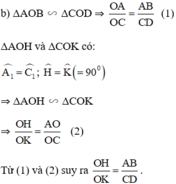
a: Xét ΔOAB và ΔOCD có
góc OAB=góc OCD
góc AOB=góc COD
=>ΔOAB đồng dạng vơi ΔOCD
=>OA/OC=OB/OD=AB/CD
=>OA*OD=OB*OC
b: OA/OC=AB/CD
=>OA/6=5/10=1/2
=>OA=3cm
Xet ΔADC có OE//DC
nên OE/DC=AO/AC
=>OE/10=3/(3+6)=3/9=1/3
=>OE=10/3cm