Bài 1: Tính Sn= 1.20+2.21+3.22+.....+n.2n-1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HH
1
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 5 2021
Ủa dấu thứ 2 là + hay trừ bạn? Là dấu trừ đúng ko?
Xét khai triển:
\(\left(-1+x\right)^{2n+1}=-C_{2021}^0+C_{2021}^1x-C_{2021}^2x^2+...+C_{2021}^{2021}x^{2021}\)
Đạo hàm 2 vế:
\(\left(2n+1\right)\left(-1+x\right)^{2n}=C_{2021}^1-2xC_{2021}^2+3x^2C_{2021}^3-...+\left(2n+1\right)x^{2n}C_{2021}^{2021}\)
Thay \(x=2\) ta được:
\(2n+1=C_{2021}^1-2.2C_{2021}^2+3.2^2C_{2021}^3-...+\left(2n+1\right)2^{2n}C_{2021}^{2021}\)
\(\Rightarrow2n+1=2005\)
\(\Rightarrow n=1002\)
CM
8 tháng 2 2018
Chọn A.
Phương pháp:
Áp dụng công thức khai triển nhị thức Newton:
CM
8 tháng 11 2017
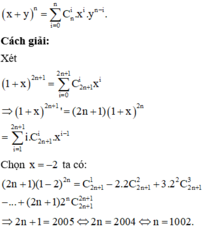
Chọn D.
Với ∀x ∈ R ta có: 
Lấy đạo hàm hai vế theo x ta được:
Thay x = -2 vào (1) ta được:
Từ yêu cầu bài toán ta có: 2n + 1 2017 ⇔ n = 2018.
DD
0
NV
Nguyễn Việt Lâm
Giáo viên
19 tháng 3 2022
1. Áp dụng công thức tổng cấp số nhân:
\(S_n=u_1.\dfrac{q^n-1}{q-1}=2.\dfrac{2^n-1}{2-1}=2.\left(2^n-1\right)=2^{n+1}-2\)
2. \(\left\{{}\begin{matrix}u_2+u_5=12\\u_4+u_8=22\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left(u_1+d\right)+\left(u_1+4d\right)=12\\\left(u_1+3d\right)+\left(u_1+7d\right)=22\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}2u_1+5d=12\\2u_1+10d=22\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}u_1=1\\d=2\end{matrix}\right.\)
\(\Rightarrow u_n=u_1+\left(n-1\right)d=1+\left(n-1\right)2=2n-1\)
\(\Rightarrow S_n=\dfrac{n\left(u_1+u_n\right)}{2}=\dfrac{n\left(1+2n-1\right)}{2}=n^2\)
3. \(\left\{{}\begin{matrix}u_1+u_2=4\\u_4+u_1=28\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}u_1+u_1q=4\\u_1q^3+u_1=28\end{matrix}\right.\)
\(\Rightarrow\dfrac{q^3+1}{q+1}=\dfrac{28}{4}\Rightarrow q^2-q+1=7\)
\(\Rightarrow q^2-q-6=0\Rightarrow\left[{}\begin{matrix}q=3\\q=-2\end{matrix}\right.\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
6 tháng 3 2023
Bài 1 :
A = 12 + 22 + 32 +....+n2
A = 12 + 2.(1+1) + 3.(2 +1) + 4.( 3 +1) +.....+n(n-1 + 1)
A = 1 + 1.2 + 2 + 2.3 + 3 + 3.4 + 4 +.....+ n.(n-1) + n
A = ( 1 + 2 + 3 + 4 +....+n) + ( 1.2 + 2.3 + 3.4 +....+(n-1).n
A = (n+1).{(n-1):n+1)/2 +1/3.[1.2.3 +2.3.3 +.....+(n-1)n.3]
A = (n+1).n/2+1/3.[1.2.3 +2.3.(4-1)+ ...+(n-1).n [(n+1) - (n -2)]
A = (n+1)n/2+1/3.( 1.2.3 + 2.3.4 -1.2.3 +..+ (n-1)n(n+1)- (n-2)(n-1)n)
A =(n+1)n/2 + 1/3.(n-1)n(n+1)
A = n(n+1)[1/2 + 1/3 .(n-1)]
A = n.(n+1) \(\dfrac{3+2n-2}{6}\)
A= n.(n+1)(2n+1)/6
Bài 2 :
a, (x+1) +(x+2) + (x+3)+...+(x+10) = 5070
(x+10 +x+1).{( x+10 - x -1): 1 +1):2 = 5070
(2x + 11)10 : 2 = 5070
( 2x + 11)5 = 5070
2x+ 11 = 5070:5
2x = 1014 - 11
2x = 1003
x = 1003 :2
x = 501,5
b, 1 + 2 + 3 +...+x = 820
( x + 1)[ (x-1):1 +1] : 2 = 820
(x +1).x = 820 x 2
(x +1).x = 1640
(x +1) .x = 40 x 41
x = 40
