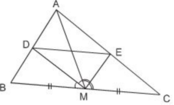
Cho tam giác ABC, đường trung tuyến AM, phân giác của góc AMB cắt AB tại E, phân giác của góc AMC cắt AC ở D. a) Chứng minh DE // BC. b) Biết ME = MD. Chứng minh tam giác ABC cân. c) biết BC=16cm và CD/DA=3/5. Tính tổng ME^2+MD^2=?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 2 2023
Xet ΔMAB có MD là phân giác
nên AD/DB=AM/MB=AM/MC
Xét ΔMAC có ME là phân giác
nên AE/EC=AM/MC
=>AD/DB=AE/EC
=>DE//BC
=>ΔADE đồng dạng với ΔABC
TB
6 tháng 8 2018
Hình bạn tự vẽ nha.
a, \(\Delta ABC\) có: AM là đường trung tuyến của \(\Delta ABC\)\(\Rightarrow BM=MC\), \(AI=\frac{2}{3}AM\)
\(\Delta AMB\)có: MD là phân giác của \(\widehat{AMB}\)\(\Rightarrow\frac{AD}{DB}=\frac{AM}{MB}\)(tính chất đường phân giác trong tam giác) (1)
\(\Delta AMC\)có: ME là phân giác của \(\widehat{AMC}\)\(\Rightarrow\frac{AE}{EC}=\frac{AM}{MC}\)(tính chất đường phân giác trong tam giác) (2)
Từ (1), (2) và \(BM=MC\left(cmt\right)\Rightarrow\frac{AD}{DB}=\frac{AE}{EC}\)
\(\Delta ABC\)có: \(\frac{AD}{DB}=\frac{AE}{EC}\left(cmt\right)\Rightarrow DE//BC\)(định lý Ta-lét đảo)
b, \(\Delta ABM\)có: \(DI//BM\left(cmt\right)\Rightarrow\frac{DI}{BM}=\frac{AI}{AM}\)(hệ quả của định lý Ta-lét) (3)
\(\Delta AMC\)có: \(IE//MC\left(cmt\right)\Rightarrow\frac{IE}{CM}=\frac{AI}{AM}\)(hệ quả của định lý Ta-lét) (4)
Từ (3), (4) và \(BM=MC\left(cmt\right)\Rightarrow DI=IE\)
c, Ta có: \(\frac{IE}{CM}=\frac{AI}{AM}\left(cmt\right)\)\(\Leftrightarrow\frac{IE}{15}=\frac{\frac{2}{3}AM}{AM}\)\(\Leftrightarrow\frac{IE}{15}=\frac{\frac{2}{3}.10}{10}\)\(\Leftrightarrow\frac{IE}{15}=\frac{2}{3}\)\(\Leftrightarrow IE=10\left(cm\right)\)
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 3 2023
Áp dụng định lý phân giác cho tam giác ABM:
\(\dfrac{AM}{BM}=\dfrac{AD}{BD}\) (1)
Áp dụng định lý phân giác cho tam giác ACM:
\(\dfrac{AM}{CM}=\dfrac{AE}{CE}\) (2)
Mà AM là trung tuyến \(\Rightarrow BM=CM\) (3)
(1);(2);(3) \(\Rightarrow\dfrac{AD}{BD}=\dfrac{AE}{CE}\Rightarrow\dfrac{AD}{AD+BD}=\dfrac{AE}{AE+CE}\Rightarrow\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
\(\Rightarrow DE||BC\) (định lý talet đảo)
14 tháng 3 2022
a: BC=2MB=90cm
Xét ΔAMB có MD là phân giác
nên AD/AM=DB/BM
=>AD/30=DB/45
=>AD/2=DB/3
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{AD}{2}=\dfrac{DB}{3}=\dfrac{AD+DB}{2+3}=\dfrac{50}{5}=10\)
Do đó: AD=20(cm); DB=30(cm)
b: Xét ΔAMB có MD là phân giác
nên AD/DB=AM/MB=AM/MC(1)
Xét ΔAMC có ME là phân giác
nên AE/EC=AM/MC(2)
Từ (1) và (2) suy ra AD/DB=AE/EC
hay DE//BC
