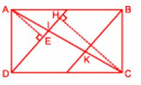
Cho hình chữ nhật ABCD, gọi M và N lần lượt là điểm chính giữa AB và CD. Nối DM,BN cắt AC tại I và K. So sánh AI=IK=KC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
7 tháng 7 2017
Ta có : dt (ABC) = 2 x dt (AMD) (vì AB = 2 x AM và AD = BC) ; dt (DCM) = dt (ABC) (vì AB = DC và c.cao cùng bằng BC)
Suy ra dt (DCM) = 2 x dt (AMD). Gọi CH và AE lần lượt là chiều cao của tam giác DCM và DAM xuống đáy DM, khi đó CH = 2 x AE. Nhưng CH và AE lần lượt là chiều cao của tam giác ICM và IAM có chung cạnh đáy IM. Vậy dt (ICM) = 2 x dt (IAM). Mà tam giác IAM và ICM chung chiều cao từ M, do đó IC = 2 x AI, suy ra AC = 3 x AI hay AI = 1/3 AC.
Làm tương tự với các cặp tam giác ABN và CBN ; KCN và KAN ta có KC = 1/3 AC. Vậy AI = KC = 1/3 AC, suy ra IK = 1/3 AC.
Do đó AI = IK = KC.
22 tháng 9 2019
bn tự kẻ hình nha!
a) ta có: AB = DC ( ACBD là hình bình hành)
----> BM = CN ( = 1/2. AB = 1/2 . DC)
mà BM // CN
-----> BMNC là h.b.h
b) xét tam giác AMD và tam giác CNB
có: AM = CN ( = 1/2.AB = 1/2.CD)
AD = BC (gt)
^DAM = ^NCB (gt)
-----> tg AMD = tg CNB (c-g-c)
-----> DM = NB ( 2 cạnh t/ ư)
c) AN cắt DM tại I, MC cắt BN tại K. chứng minh : AC,BD,MN,IK
bài làm
Gọi AC cắt DB tại E
ta có: tg AMD = tg CNB (cmt)
-----> ^AMD = ^CNB
mà ^AMD = ^MDN ( AB//DC)
-----> ^CNB = ^MDN
mà ^CNB, ^MDN nằm ở vị trí đồng vị
-----> DM// BN
và DM = BN (pb)
-----> DMBN là h.b.h
-------> BD cắt MN tại E ( do 2 đường chéo của h.b.h cắt nhau tại trung điểm của mỗi đường)
tương tự bn cx chứng minh: MINK là h.b.h ( MI = NK = 1/2.DM = 1/2.BN)
-----> MN cắt IK tại E
------------> AC,BD, MN,IK đồng quy tại E
