Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
1: ΔOAB cân tại O
mà OI là trung tuyến
nên OI vuông góc AB
góc OIM=góc OCM=góc ODM=90 độ
=>O,I,M,D,C cùng thuộc đường tròn đường kính OM
góc DIM=góc MOD
góc CIM=góc COM
mà góc COM=góc DOM
nên góc DIM=góc CIM
=>IM là phân giác của góc CID
a) Trong (O) có AB là dây cung không đi qua O và I là trung điểm AB
\(\Rightarrow OI\bot AB\Rightarrow\angle MIO=90\Rightarrow\angle MIO+\angle MCO=90+90=180\)
\(\Rightarrow MIOC\) nội tiếp
b) Vì MC,MD là tiếp tuyến \(\Rightarrow\Delta MCD\) cân tại M có MO là phân giác \(\angle CMD\) \(\Rightarrow MO\bot CD\) mà \(EF\parallel CD\) \(\Rightarrow EF\bot MO\)
tam giác MOE vuông tại O có đường cao OC \(\Rightarrow CM.CE=OC^2\)
tam giác MOC vuông tại C có đường cao HC \(\Rightarrow OH.OM=OC^2\)
\(\Rightarrow OH.OM=CM.CE\)
Vì H là trung điểm CD (\(\Delta MCD\) cân tại M) và \(EF\parallel CD\)
\(\Rightarrow O\) là trung điểm EF
\(\Rightarrow S_{MEF}=2S_{MOE}=2.\dfrac{1}{2}.OC.ME=OC.\left(CM+CE\right)\)
\(\ge R.\sqrt{CM.CE}=R.2\sqrt{OC^2}=R.2OC=2R^2\)
\(\Rightarrow S_{MEF_{min}}=2R^2\) khi \(CM=CE=R\left(CM.CE=R^2\right)\)
\(\Rightarrow OM=\sqrt{R^2+R^2}=\sqrt{2}R\)
Vậy M nằm trên d sao cho \(OM=\sqrt{2}R\) thì diện tích tam giác MEF nhỏ nhất \(\left(=2R^2\right)\)
d) Ta có:
K là trung điểm của CE (E đối xứng với C qua AB)
K là trung điểm của AB
AB ⊥ CE (MO ⊥ AB)
⇒ Tứ giác AEBC là hình thoi
⇒ BE // AC
Mà AC ⊥ AD (A thuộc đường tròn đường kính CD)
Nên BE ⊥ AD và DK ⊥ AB
Vậy E là trực tâm của tam giác ADB
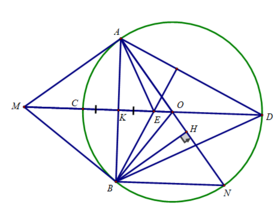
Dễ thấy tứ giác OAMB nội tiếp (1) (do có \(\widehat{OAM}=\widehat{OBM}=90^o\))
Xét đường tròn (O), có I là trung điểm của dây cung CD \(\Rightarrow OI\perp CD\) tại I hay \(\widehat{OEM}=90^o\)
Từ đó suy ra tứ giác OEMB nội tiếp (2) (\(\widehat{OEM}=\widehat{OBM}=90^o\))
Từ (1) và (2), suy ra 5 điểm O,A,B,M,E cùng nằm trên 1 đường tròn \(\Rightarrow\)Tứ giác AOEB nội tiếp.