Cho ( P ) y = x^2 và ( d ) y = -3x + 4
a) vẽ đồ thị 2 hàm số trên cùng một mặt phẳng toạ độ.
b) tìm toạ độ giao điểm của ( P ) và ( d ) bằng phép tính.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
21 tháng 11 2021
b. PTHDGD: \(2x=x+1\Leftrightarrow x=1\Leftrightarrow y=2\Leftrightarrow A\left(1;2\right)\)
Vậy tọa độ giao điểm 2 đt là \(A\left(1;2\right)\)
22 tháng 3 2023
a: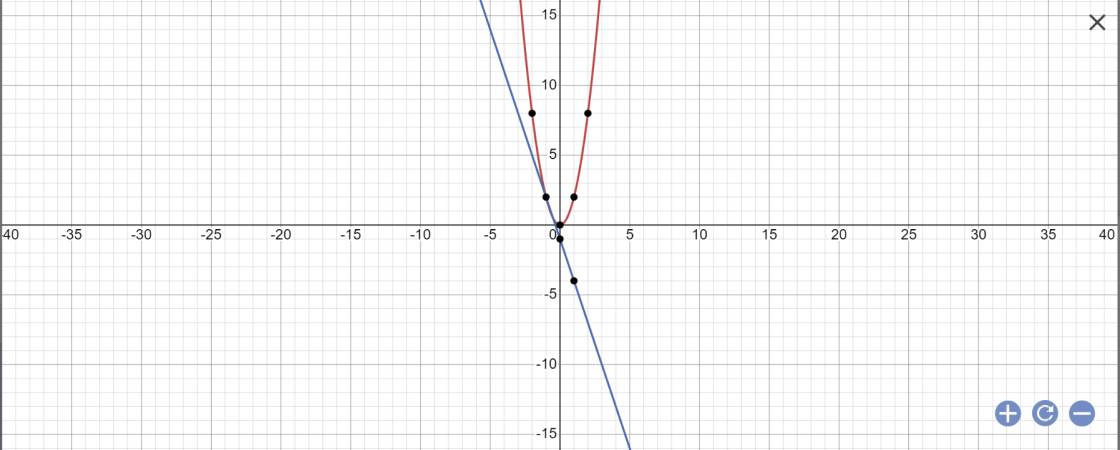 
b: PTHĐGĐ là:
2x^2+3x+1=0
=>x=-1 hoặc x=-1/2
=>y=2 hoặc y=1/2
Y
22 tháng 3 2023
\(a,\) Tự vẽ nha
\(b,\) Gọi \(A\left(x_A;y_A\right);B\left(x_B;y_B\right)\) là tọa độ của \(\left(P\right)\) và \(\left(d\right)\)
Ta có : \(\left(P\right)=\left(d\right)\)
Suy ra :
\(2x^2=-3x-1\)
\(\Leftrightarrow2x^2+3x+1=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=-\dfrac{1}{2}\\x_2=-1\end{matrix}\right.\)
Thay \(x_1=-\dfrac{1}{2}\) vào \(\left(P\right):y=2x^2\Rightarrow y=2.\left(-\dfrac{1}{2}\right)^2=\dfrac{1}{2}\)
Thay \(x_2=-1\) vào \(\left(d\right):y=-3x-1\Rightarrow y=-3.\left(-1\right)-1=2\)
Vậy tọa độ của 2 đồ thị hàm số là \(A\left(-\dfrac{1}{2};\dfrac{1}{2}\right);B\left(-1;2\right)\)
Y
22 tháng 3 2023
\(a,\) Tự vẽ nhaa
\(b,\) Gọi \(A\left(x_A;y_A\right);B\left(x_B;y_B\right)\) là tọa độ giao điểm của \(\left(P\right)\) và \(\left(d\right)\)
Ta có : \(\left(P\right)=\left(d\right)\)
Suy ra :
\(2x^2=-3x+1\)
\(\Leftrightarrow2x^2+3x-1=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{-3+\sqrt{17}}{4}\\x_2=\dfrac{-3-\sqrt{17}}{4}\end{matrix}\right.\)
Thay \(x_1=\dfrac{-3+\sqrt{17}}{4}\) vào \(\left(P\right):y=2x^2\Rightarrow y=2.\left(\dfrac{-3+\sqrt{17}}{4}\right)=\dfrac{-3+\sqrt{17}}{2}\)
Thay \(x_2=\dfrac{-3-\sqrt{17}}{4}\) vào \(\left(d\right):y=-3x+1\Rightarrow y=-3.\left(\dfrac{-3-\sqrt{17}}{4}\right)+1=\dfrac{13+3\sqrt{17}}{4}\)
Vậy toa độ giao điểm của 2 đồ thị hàm số là
\(A\left(\dfrac{-3+\sqrt{17}}{4};\dfrac{-3+\sqrt{17}}{2}\right)\) và \(B\left(\dfrac{-3-\sqrt{17}}{4};\dfrac{13+3\sqrt{17}}{4}\right)\)
10 tháng 5 2022
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}3x^2-2x-1=0\\y=3x^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x^2-3x+x-1=0\\y=3x^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-1\right)\left(3x+1\right)=0\\y=3x^2\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(1;3\right);\left(-\dfrac{1}{3};\dfrac{1}{3}\right)\right\}\)
8 tháng 3 2022
a, bạn tự vẽ
b, Hoành độ giao điểm tm pt
\(x^2+x-2=0\)ta có a + b + c = 1 + 1 - 2 = 0
Vậy pt có 2 nghiệm x = 1 ; x = 2
Với x = 1 => y = -1
Với x = 2 => y = -4
Vậy (P) cắt (d) tại A(1;-1) ; B(2;-4)
30 tháng 5 2021
a)Tự vẽ
b) Xét pt hoành độ gđ của (P) và (d) có:
\(\dfrac{3}{2}x^2=x+\dfrac{1}{2}\)
\(\Leftrightarrow3x^2-2x-1=0\) \(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\Rightarrow y=\dfrac{3}{2}.\left(-\dfrac{1}{3}\right)^2=\dfrac{1}{6}\\x=1\Rightarrow y=\dfrac{3}{2}\end{matrix}\right.\)
Vậy gđ của (d) và (P) là \(\left(-\dfrac{1}{3};\dfrac{1}{6}\right),\left(1;\dfrac{3}{2}\right)\)
c) Gọi đt cần tìm có dạng (d') \(y=ax+b\) (a2+b2>0)
Gọi A(-4;y1) và B(2;y2) là hai giao điểm của (P) và (d')
\(A;B\in\left(P\right)\Rightarrow\left\{{}\begin{matrix}y_1=24\\y_2=6\end{matrix}\right.\)
\(\Rightarrow A\left(-4;24\right),B\left(2;6\right)\) \(\in\left(d'\right)\)
\(\Rightarrow\left\{{}\begin{matrix}24=-4a+b\\6=2a+b\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a=-3\\b=12\end{matrix}\right.\) (thỏa)
Vậy (d'): y=-3x+12
b: PTHĐGĐ là:
x^2+3x-4=0
=>(x+4)(x-1)=0
=>x=-4 hoặc x=1
=>y=16 hoặc y=1